
分析 (Ⅰ)由椭圆的离心率为$\frac{1}{2}$,且过点$(1,\frac{3}{2})$,列出方程组,求出a,b,c,由此能求出椭圆方程.
(II)联立方程$\left\{{\begin{array}{l}{y=\frac{3}{2}x+m}\\{\frac{x^2}{4}+\frac{y^2}{3}=1}\end{array}}\right.$,得3x2+3mx+m2-3=0,由此利用根的判别式、韦达定理、直线方程,结合已知条件能求出m的值.
解答 解:(Ⅰ)由题意得:$\left\{{\begin{array}{l}{{a^2}={b^2}+{c^2}}\\{e=\frac{c}{a}=\frac{1}{2}}\\{\frac{1}{a^2}+\frac{9}{{4{b^2}}}=1}\end{array}}\right.$,(2分)
解得$a=2,b=\sqrt{3},c=1$,(4分)
∴椭圆方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$.(5分)
(II)设C(x1,y1),D(x2,y2),
联立方程$\left\{{\begin{array}{l}{y=\frac{3}{2}x+m}\\{\frac{x^2}{4}+\frac{y^2}{3}=1}\end{array}}\right.$,得3x2+3mx+m2-3=0①,
∴判别式△=(3m)2-12(m2-3)=-3m2+36>0,解得m2<12,(7分)
∵x1,x2为①式的根,∴${x_1}+{x_2}=-m,{x_1}{x_2}=-\frac{{{m^2}-3}}{3}$,(8分)
由题意知A(-2,0),B(2,0),∴${k_{AD}}={k_1}=\frac{y_2}{{{x_2}+2}},{k_{BC}}={k_2}=\frac{y_1}{{{x_1}-2}}$.
∵k1:k2=2:1,即$\frac{{{y_2}({x_1}-2)}}{{{y_1}({x_2}+2)}}=\frac{2}{1}$,得$\frac{{y_2^2{{({x_1}-2)}^2}}}{{y_1^2{{({x_2}+2)}^2}}}=4$②,
又$\frac{{{x}_{1}}^{2}}{4}+\frac{{{y}_{1}}^{2}}{3}=1$,∴${{y}_{1}}^{2}=\frac{3}{4}(4-{{x}_{1}}^{2})$,同理${{y}_{2}}^{2}=\frac{3}{4}(4-{{x}_{2}}^{2})$,(10分)
代入②式,解得$\frac{(2-{x}_{2})(2-{x}_{1})}{(2+{x}_{1})(2+{x}_{2})}$=4,即10(x1+x2)+3x1x2+12=0,
∴10(-m)+m2-3+12=0,解得m=1或m=9,
又∵m2<12,∴m=9(舍去),∴m=1.(12分)
点评 本题考查椭圆方程的求法,考查满足条件的实数值的求法,解题时要认真审题,注意根的判别式、韦达定理、直线方程的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8个 | B. | 4个 | C. | 2个 | D. | 0个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某篮球队对篮球运动员的篮球技能进行统计研究,针对篮球运动员在投篮命中时,运动员在篮筐中心的水平距离这项指标,对某运动员进行了若干场次的统计,依据统计结果绘制如下频率分布直方图:
某篮球队对篮球运动员的篮球技能进行统计研究,针对篮球运动员在投篮命中时,运动员在篮筐中心的水平距离这项指标,对某运动员进行了若干场次的统计,依据统计结果绘制如下频率分布直方图:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
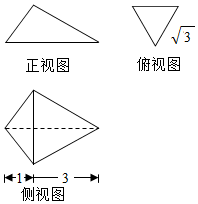
| A. | $\frac{16π}{3}$ | B. | $\frac{32π}{3}$ | C. | 4$\sqrt{3}$ | D. | 16π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com