
 某篮球队对篮球运动员的篮球技能进行统计研究,针对篮球运动员在投篮命中时,运动员在篮筐中心的水平距离这项指标,对某运动员进行了若干场次的统计,依据统计结果绘制如下频率分布直方图:
某篮球队对篮球运动员的篮球技能进行统计研究,针对篮球运动员在投篮命中时,运动员在篮筐中心的水平距离这项指标,对某运动员进行了若干场次的统计,依据统计结果绘制如下频率分布直方图:分析 (I) 设该运动员到篮筐的水平距离的中位数为x,推导出0.40×(5-x)+0.20×1=0.5,由此能求出该运动员到篮筐的水平距离的中位数.
(2)由频率分布直方图得投篮命中时距离篮筐距离超过4米的概率为p=$\frac{3}{5}$,随机变量ξ的所有可能取值为-4,-2,0,2,4,分别求出相应的概率,由此能求出X的分布列和EX.
解答 解:(I) 设该运动员到篮筐的水平距离的中位数为x,
∵0.05×2+0.10+0.20<0.5,且(0.40+0.20)×1=0.6>0.5,
∴x∈[4,5]…(2分)
由0.40×(5-x)+0.20×1=0.5,解得x=4.25,
∴该运动员到篮筐的水平距离的中位数是4.25(米).
(Ⅱ)由频率分布直方图得投篮命中时距离篮筐距离超过4米的概率为p=$\frac{3}{5}$,
随机变量ξ的所有可能取值为-4,-2,0,2,4,…(8分)
$P({X=-4})={({\frac{2}{5}})^4}=\frac{16}{625}$,
$P(X=2)=C_4^3{(\frac{2}{5})^1}{(\frac{3}{5})^3}=\frac{216}{625}$,
$P(X=-2)=C_4^1{(\frac{2}{5})^3}(\frac{3}{5})=\frac{96}{625}$,
$P(X=0)=C_4^2{(\frac{2}{5})^2}{(\frac{3}{5})^2}=\frac{216}{625}$,
$P(X=2)=C_4^3{(\frac{2}{5})^1}{(\frac{3}{5})^3}=\frac{216}{625}$,
$P({X=4})={({\frac{3}{5}})^4}=\frac{81}{625}$,
∴X的分布列为:
| X | -4 | -2 | 0 | 2 | 4 |
| P | $\frac{16}{625}$ | $\frac{96}{625}$ | $\frac{216}{625}$ | $\frac{216}{625}$ | $\frac{81}{625}$ |
点评 本题考查中位数的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意排列组合知识的合理运用.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案科目:高中数学 来源: 题型:解答题
 如图,直三棱柱ABC-A1B1C1中,D是AB的中点.
如图,直三棱柱ABC-A1B1C1中,D是AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{4}{3}$ | B. | $-\frac{5}{3}$ | C. | $-\frac{3}{5}$ | D. | $-\frac{5}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5条 | B. | 7条 | C. | 9条 | D. | 11条 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
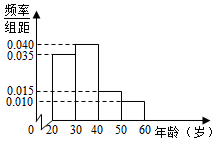 某学校有120名教师,且年龄都在20岁到60岁之间,各年龄段人数按分组,其频率分布直方图如图所示,学校要求每名教师都要参加两项培训,培训结束后进行结业考试.已知各年龄段两项培训结业考试成绩优秀的人数如表示,假设两项培训是相互独立的,结业考试成绩也互不影响.
某学校有120名教师,且年龄都在20岁到60岁之间,各年龄段人数按分组,其频率分布直方图如图所示,学校要求每名教师都要参加两项培训,培训结束后进行结业考试.已知各年龄段两项培训结业考试成绩优秀的人数如表示,假设两项培训是相互独立的,结业考试成绩也互不影响.| 年龄分组 | A项培训成绩优秀人数 | B项培训成绩优秀人数 |
| [20,30) | 30 | 18 |
| [30,40) | 36 | 24 |
| [40,50) | 12 | 9 |
| [50,60] | 4 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com