Question

4．如图，直三棱柱ABC-A₁B₁C₁中，D是AB的中点．
（1）证明：BC₁∥平面A₁CD；
（2）设AA₁=AC=CB=2，AB=2$\sqrt{2}$，求异面直线BC₁与A₁D所成角的大小．

Answer 1

分析 （1）根据线面平行的判定定理即可证明BC₁∥平面A₁CD；
（2）根据异面直线所成角的定义进行求解即可．

解答 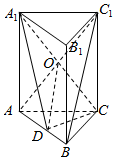（1）证明：连结AC₁，交A₁C于点O，连结OD，
因为D是AB的中点，所以BC₁∥OD，
因为BC₁?平面A₁CD，OD?平面A₁CD，
所以BC₁∥平面A₁CD．
（2）解：结合（1）易知∠A₁DO即为异面直线A与D，E所成角，
因为AC=BC，D为AB的中点，所以CD⊥AB，
又因为该三棱柱是直三棱柱，所以CD⊥平面ABB₁A₁，
即CD⊥平面A₁DE，∵$A{A_1}=AC=CB=2，AB=2\sqrt{2}$，
∴${A_1}D=\sqrt{6}，DO={A_1}O=\frac{1}{2}{A_1}C=\sqrt{2}$，
∴$cos∠{A_1}DO=\frac{{\sqrt{3}}}{2}$，∴$∠{A_1}DO=\frac{π}{6}$．

点评 本题主要考查线面平行的判定以及异面直线所成角的求解，利用相应的判定定理以及异面直线所成角的定义是解决本题的关键．