
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,4) |
分析 方程的解所在的区间,则对应的函数的零点在这个范围,把原函数写出两个初等函数,即两个初等函数的交点在这个区间,结合两个函数的草图得到函数的交点的位置在(1,3),再进行进一步检验.
解答 解:∵方程log3x=-x+3的解,
根据两个基本函数的图象可知两个函数的交点一定在(1,3),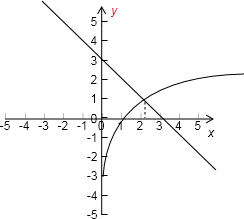
因m(x)=log3x+x-3在(1,2)上不满足m(1)m(2)<0,
方程 log3x+x-3=0 的解所在的区间是(2,3),
即则x0所在的区间是(2,3),
故选:C.
点评 本题考查函数零点的检验,考查函数与对应的方程之间的关系,是一个比较典型的函数的零点的问题,注意解题过程中数形结合思想的应用.属基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{4}$) | B. | ($\frac{1}{4}$,$\frac{1}{2}$) | C. | ($\frac{1}{2}$,$\frac{3}{4}$) | D. | ($\frac{3}{4}$,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
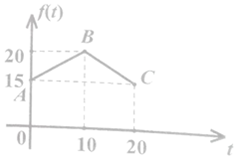 经过市场调查,某门市部的一种小商品在过去的20天内的销售量(件)与价格(元)均为时间t (天)的函数,且日销售量近似满足g(t)=80-2t (件),而日销售量价格近似满足函数f(t),且f(t)的图象为如图所示的两线段AB,BC.
经过市场调查,某门市部的一种小商品在过去的20天内的销售量(件)与价格(元)均为时间t (天)的函数,且日销售量近似满足g(t)=80-2t (件),而日销售量价格近似满足函数f(t),且f(t)的图象为如图所示的两线段AB,BC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com