
【题目】已知![]() ,
,![]() 分别是
分别是![]() 的边
的边![]() ,
,![]() 上的一点,
上的一点,![]() ,将
,将![]() 沿
沿![]() 折起为
折起为![]() ,使
,使![]() 点位于
点位于![]() 点的位置,连接
点的位置,连接![]() ,
,![]() ,
,![]() .
.
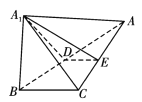
(1)若![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,平面
的中点,平面![]() 与平面
与平面![]() 的交线为
的交线为![]() ,证明:
,证明:![]() ;
;
(2)若平面![]() 平面
平面![]() ,
,![]() 与
与![]() 的面积分别为4和9,
的面积分别为4和9,![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
【答案】(1)证明见解析(2)![]()
【解析】
(1)根据图形的关系可得![]() ,从而得到角的关系
,从而得到角的关系![]() ,即
,即![]() ,同理得
,同理得![]() ,根据线面垂直判定定理可得
,根据线面垂直判定定理可得![]() 平面
平面![]() ,即可得到
,即可得到![]() ,由线面平行性质定理可得
,由线面平行性质定理可得![]() ,进而得结论;
,进而得结论;
(2)过点![]() 在平面
在平面![]() 内作
内作![]() ,垂足为
,垂足为![]() ,交
,交![]() 于
于![]() ,连接
,连接![]() ,
,![]() ,运用面面垂直的性质定理以及线面垂直的判断和性质,结合三角形的面积公式和三角形的相似,以及勾股定理和棱锥的体积公式,计算可得所求值.
,运用面面垂直的性质定理以及线面垂直的判断和性质,结合三角形的面积公式和三角形的相似,以及勾股定理和棱锥的体积公式,计算可得所求值.
(1)因为![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,
的中点,![]() 沿
沿![]() 折起为
折起为![]() ,
,
所以![]() ,
,
所以![]() ,
,![]() ,
,
所以![]() ,所以
,所以![]() .
.
又![]() ,同理有
,同理有![]() ,
,
而![]() ,所以
,所以![]() 平面
平面![]() .
.
而![]() 平面
平面![]() ,所以
,所以![]() ,
,
又![]() 为平面
为平面![]() 与平面
与平面![]() 的交线,所以
的交线,所以![]() ,所以
,所以![]() .
.
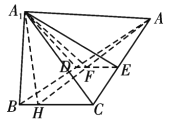
(2)如图所示,过点![]() 在平面
在平面![]() 内作
内作![]() ,垂足为
,垂足为![]() ,交
,交![]() 于
于![]() ,连接
,连接![]() ,
,![]() .
.
因为平面![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .而
.而![]() 平面
平面![]() ,所以
,所以![]() .
.
由![]() ,易知
,易知![]() ,而
,而![]() 沿
沿![]() 折起为
折起为![]() ,所以
,所以![]() .
.
所以![]() 平面
平面![]() ,所以
,所以![]() ,由此
,由此![]() ,
,
所以![]() 平面
平面![]() ,而
,而![]() 平面
平面![]() ,所以
,所以![]() .
.
由已知,![]() 与
与![]() 的面积分别为4和9,
的面积分别为4和9,![]() ,易求
,易求![]() ,
,
由![]() ,可得
,可得![]() ,所以
,所以![]() ,
,
在![]() 中,
中,![]() ,
,![]() .
.
所以![]() ,
,
故三棱锥![]() 的体积
的体积
![]() .
.


 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:
【题目】已知集合A={1,2,3,4,5,6,7,8,9),在集合A中任取三个元素,分别作为一个三位数的个位数,十位数和百位数,记这个三位数为a,现将组成a的三个数字按从小到大排成的三位数记为I(a),按从大到小排成的三位数记为D(a)(例如a=219,则I(a)=129,D(a)=921),阅读如图所示的程序框图,运行相应的程序,任意输入一个a,则输出b的值为( )
A. 792 B. 693 C. 594 D. 495
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为原点,极轴为
,以极点为原点,极轴为![]() 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线![]() 过点
过点![]() ,倾斜角为
,倾斜角为![]() .
.
(1)求曲线![]() 的直角坐标方程与直线l的参数方程;
的直角坐标方程与直线l的参数方程;
(2)设直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为F,过点F,斜率为1的直线与抛物线C交于点A,B,且
的焦点为F,过点F,斜率为1的直线与抛物线C交于点A,B,且![]() .
.
(1)求抛物线C的方程;
(2)过点Q(1,1)作直线交抛物线C于不同于R(1,2)的两点D、E,若直线DR,ER分别交直线![]() 于M,N两点,求|MN|取最小值时直线DE的方程.
于M,N两点,求|MN|取最小值时直线DE的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x-lnx,g(x)=x2-ax.
(1)求函数f(x)在区间[t,t+1](t>0)上的最小值m(t);
(2)令h(x)=g(x)-f(x),A(x1,h(x1)),B(x2,h(x2))(x1≠x2)是函数h(x)图像上任意两点,且满足![]() >1,求实数a的取值范围;
>1,求实数a的取值范围;
(3)若x∈(0,1],使f(x)≥![]() 成立,求实数a的最大值.
成立,求实数a的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=eax﹣x﹣1,且f(x)≥0.
(1)求a;
(2)在函数f(x)的图象上取定两点A(x1,f(x1)),B(x2,f(x2))(x1<x2),记直线AB的斜率为k,问:是否存在x0∈(x1,x2),使f'(x0)=k成立?若存在,求出x0的值(用x1,x2表示);若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某搜索引擎广告按照付费价格对搜索结果进行排名,点击一次付费价格排名越靠前,被点击的次数也可能会提高,已知某关键词被甲、乙等多个公司竞争,其中甲、乙付费情况与每小时点击量结果绘制成如下的折线图.
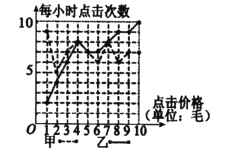
(1)试根据所给数据计算每小时点击次数的均值方差并分析两组数据的特征;
(2)若把乙公司设置的每次点击价格为x,每小时点击次数为y,则点(x,y)近似在一条直线附近.试根据前5次价格与每小时点击次数的关系,求y关于x的回归直线![]() .(附:回归方程系数公式:
.(附:回归方程系数公式: )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com