
【题目】已知函数f(x)=eax﹣x﹣1,且f(x)≥0.
(1)求a;
(2)在函数f(x)的图象上取定两点A(x1,f(x1)),B(x2,f(x2))(x1<x2),记直线AB的斜率为k,问:是否存在x0∈(x1,x2),使f'(x0)=k成立?若存在,求出x0的值(用x1,x2表示);若不存在,请说明理由.
【答案】(1)a=1(2)存在;![]()
【解析】
(1)当![]() 时,判断出
时,判断出![]() 不恒成立.当
不恒成立.当![]() 时,利用导数求得
时,利用导数求得![]() 的最小值,根据这个最小值为非负数,构造函数并结合导数,求得
的最小值,根据这个最小值为非负数,构造函数并结合导数,求得![]() 的值.
的值.
(2)首先求得![]() 的表达式,构造函数
的表达式,构造函数![]() ,由
,由![]() ,结合零点存在性定理,判断出
,结合零点存在性定理,判断出![]() 存在,并求得
存在,并求得![]() 的值.
的值.
(1)若a≤0,则对一切x>0,f(x)=eax﹣x﹣1<0,不符合题意,
若a>0,f′(x)=aeax﹣1,令f′(x)=aeax﹣1=0可得x![]() ,
,
当x![]() 时,f′(x)<0,函数f(x)单调递减,当x
时,f′(x)<0,函数f(x)单调递减,当x![]() 时,f′(x)>0,函数f(x)单调递增,
时,f′(x)>0,函数f(x)单调递增,
故当x![]() 时,函数取得最小值f(
时,函数取得最小值f(![]() )
)![]() ,
,
由题意可得,有![]() 0①,
0①,
令g(t)=t﹣tlnt﹣1,则g′(t)=﹣lnt,
当0<t<1时,g′(t)>0,g(t)单调递增,当t>1时,g′(t)<0,g(t)单调递减,
故当t=1时,g(t)取得最大值g(1)=0,当且仅当![]() 1即a=1时①成立,
1即a=1时①成立,
综上a=1;
(2)由题意可知,k![]() 1,
1,
令t(x)=f′(x)﹣k=ex![]() ,则可知y=t(x)在[x1,x2]上单调递增,
,则可知y=t(x)在[x1,x2]上单调递增,
且t(x1)![]() [
[![]() (x2﹣x1)﹣1],t(x2)
(x2﹣x1)﹣1],t(x2)![]() [e
[e![]() (x1﹣x2)﹣1],
(x1﹣x2)﹣1],
由(1)可知f(x)=ex﹣x﹣1≥0,x=0时取等号,
∴![]() (x2﹣x1)﹣1≥0,e
(x2﹣x1)﹣1≥0,e![]() (x1﹣x2)﹣1≥0,
(x1﹣x2)﹣1≥0,
∴t(x1)<0,t(x2)>0,
由零点判定定理可得,存在x0∈(x1,x2),使得t(x0)=0且由![]() 解得
解得![]() ,
,
综上可得,存在x0∈(x1,x2),使f'(x0)=k成立


科目:高中数学 来源: 题型:
【题目】某单位共有职工2000人,其中男职工1200人,女职工800人为调查2019年“双十一”购物节的消费情况,按照性别采用分层抽样的方法抽取了该单位100人在“双十一”当天网络购物的消费金额(单位:百元),其频率分布直方图如下:

(1)已知抽取的样本中,有3名女职工的消费不低于1000元,现从消费不低于1000元的职工中抽取3名职工进行购物指导,求抽取的3名职工中至少有两名女职工的概率;
(2)在“双十一”当天网络购物消费金额不低于600元者称为“购物狂”,低于600元者称为“理性购物者”.已知在抽取的样本中有18名女职工消费不低于600元,请完成上图中的列联表,并判断能否有99%的把握认为“是不是购物狂”与性别有关.
附:参考数据与公式
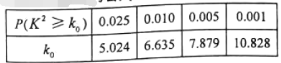
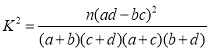
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 分别是
分别是![]() 的边
的边![]() ,
,![]() 上的一点,
上的一点,![]() ,将
,将![]() 沿
沿![]() 折起为
折起为![]() ,使
,使![]() 点位于
点位于![]() 点的位置,连接
点的位置,连接![]() ,
,![]() ,
,![]() .
.
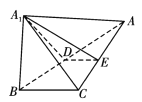
(1)若![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,平面
的中点,平面![]() 与平面
与平面![]() 的交线为
的交线为![]() ,证明:
,证明:![]() ;
;
(2)若平面![]() 平面
平面![]() ,
,![]() 与
与![]() 的面积分别为4和9,
的面积分别为4和9,![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代有着辉煌的数学研究成果,其中《周髀算经》、《九章算术》、《海岛算经》、《孙子算经》、《缉古算经》有着丰富多彩的内容,是了解我国古代数学的重要文献.这5部专著中有3部产生于汉、魏、晋、南北朝时期.现拟从这5部专著中选择2部作为学生课外兴趣拓展参考书目,则所选2部专著中至少有一部不是汉、魏、晋、南北朝时期专著的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
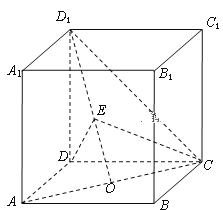
【题目】在棱长为![]() 的正方体
的正方体![]() 中,O是AC的中点,E是线段D1O上一点,且D1E=λEO.
中,O是AC的中点,E是线段D1O上一点,且D1E=λEO.
(1)若λ=1,求异面直线DE与CD1所成角的余弦值;
(2)若平面CDE⊥平面CD1O,求λ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() ,
,![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的坐标方程为
的坐标方程为![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 相切.
相切.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)在曲线![]() 上取两点
上取两点![]() 、
、![]() 于原点
于原点![]() 构成
构成![]() ,且满足
,且满足![]() ,求面积
,求面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年底,北京2022年冬奥组委会启动志愿者全球招募,仅一个月内报名人数便突破60万,其中青年学生约有50万人.现从这50万青年学生志愿者中,按男女分层抽样随机选取20人进行英语水平测试,所得成绩(单位:分)统计结果用茎叶图记录如下:

(Ⅰ)试估计在这50万青年学生志愿者中,英语测试成绩在80分以上的女生人数;
(Ⅱ)从选出的8名男生中随机抽取2人,记其中测试成绩在70分以上的人数为X,求![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)为便于联络,现将所有的青年学生志愿者随机分成若干组(每组人数不少于5000),并在每组中随机选取![]() 个人作为联络员,要求每组的联络员中至少有1人的英语测试成绩在70分以上的概率大于90%.根据图表中数据,以频率作为概率,给出
个人作为联络员,要求每组的联络员中至少有1人的英语测试成绩在70分以上的概率大于90%.根据图表中数据,以频率作为概率,给出![]() 的最小值.(结论不要求证明)
的最小值.(结论不要求证明)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com