
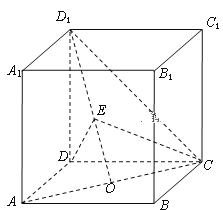
【题目】在棱长为![]() 的正方体
的正方体![]() 中,O是AC的中点,E是线段D1O上一点,且D1E=λEO.
中,O是AC的中点,E是线段D1O上一点,且D1E=λEO.
(1)若λ=1,求异面直线DE与CD1所成角的余弦值;
(2)若平面CDE⊥平面CD1O,求λ的值.
【答案】(1)![]() (2)λ=2
(2)λ=2
【解析】分析:以![]() 为单位正交基底建立如图所示的空间直角坐标系
为单位正交基底建立如图所示的空间直角坐标系![]() ,写出各点的坐标,
,写出各点的坐标,
(1)求出异面直线![]() 与
与![]() 1的方向向量用数量积公式两线夹角的余弦值(或补角的余弦值)
1的方向向量用数量积公式两线夹角的余弦值(或补角的余弦值)
(2)求出两个平面的法向量,由于两个平面垂直,故它们的法向量的内积为0,由此方程求参数![]() 的值即可.
的值即可.
详解:
(1)以![]() 为单位正交基底建立如图所示的空间直角坐标系
为单位正交基底建立如图所示的空间直角坐标系![]() .
.
则A(1,0,0),![]() ,
,![]() ,D1(0,0,1),
,D1(0,0,1),
E![]() ,
,
于是![]() ,
,![]() .
.
由cos![]() =
=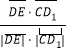 =
=![]() .
.
所以异面直线AE与CD1所成角的余弦值为![]() .
.
(2)设平面CD1O的向量为m=(x1,y1,z1),由m·![]() =0,m·
=0,m·![]() =0
=0
得  取x1=1,得y1=z1=1,即m=(1,1,1) . ………8分
取x1=1,得y1=z1=1,即m=(1,1,1) . ………8分
由D1E=λEO,则E![]() ,
,![]() =
=![]() .10分
.10分
又设平面CDE的法向量为n=(x2,y2,z2),由n·![]() =0,n·
=0,n·![]() =0.
=0.
得  取x2=2,得z2=-λ,即n=(-2,0,λ) .12分
取x2=2,得z2=-λ,即n=(-2,0,λ) .12分
因为平面CDE⊥平面CD1F,所以m·n=0,得![]() .
.


科目:高中数学 来源: 题型:
【题目】某地区现有一个直角梯形水产养殖区ABCD,∠ABC=90°,AB∥CD,AB=800m,BC=1600m,CD=4000m,在点P处有一灯塔(如图),且点P到BC,CD的距离都是1200m,现拟将养殖区ACD分成两块,经过灯塔P增加一道分隔网EF,在△AEF内试验养殖一种新的水产品,当△AEF的面积最小时,对原有水产品养殖的影响最小.设AE=d.
(1)若P是EF的中点,求d的值;
(2)求对原有水产品养殖的影响最小时的d的值,并求△AEF面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为原点,极轴为
,以极点为原点,极轴为![]() 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线![]() 过点
过点![]() ,倾斜角为
,倾斜角为![]() .
.
(1)求曲线![]() 的直角坐标方程与直线l的参数方程;
的直角坐标方程与直线l的参数方程;
(2)设直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x-lnx,g(x)=x2-ax.
(1)求函数f(x)在区间[t,t+1](t>0)上的最小值m(t);
(2)令h(x)=g(x)-f(x),A(x1,h(x1)),B(x2,h(x2))(x1≠x2)是函数h(x)图像上任意两点,且满足![]() >1,求实数a的取值范围;
>1,求实数a的取值范围;
(3)若x∈(0,1],使f(x)≥![]() 成立,求实数a的最大值.
成立,求实数a的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=eax﹣x﹣1,且f(x)≥0.
(1)求a;
(2)在函数f(x)的图象上取定两点A(x1,f(x1)),B(x2,f(x2))(x1<x2),记直线AB的斜率为k,问:是否存在x0∈(x1,x2),使f'(x0)=k成立?若存在,求出x0的值(用x1,x2表示);若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某搜索引擎广告按照付费价格对搜索结果进行排名,点击一次付费价格排名越靠前,被点击的次数也可能会提高,已知某关键词被甲、乙等多个公司竞争,其中甲、乙付费情况与每小时点击量结果绘制成如下的折线图.
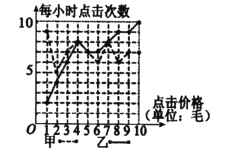
(1)试根据所给数据计算每小时点击次数的均值方差并分析两组数据的特征;
(2)若把乙公司设置的每次点击价格为x,每小时点击次数为y,则点(x,y)近似在一条直线附近.试根据前5次价格与每小时点击次数的关系,求y关于x的回归直线![]() .(附:回归方程系数公式:
.(附:回归方程系数公式: )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 上的点,
上的点,![]() 的面积最大值为
的面积最大值为![]() ,直线
,直线![]() 与
与![]() 交于
交于![]() 两点,且
两点,且![]() (
(![]() 为坐标原点)
为坐标原点)
(1)求椭圆![]() 的方程;
的方程;
(2)求证:![]() 到直线
到直线![]() 的距离为定值,并求其定值.
的距离为定值,并求其定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 指数是用体重公斤数除以身高米数的平方得出的数字,是国际上常用的衡量人体胖瘦程度以及是否健康的一个标准.对于高中男体育特长生而言,当
指数是用体重公斤数除以身高米数的平方得出的数字,是国际上常用的衡量人体胖瘦程度以及是否健康的一个标准.对于高中男体育特长生而言,当![]() 数值大于或等于20.5时,我们说体重较重,当
数值大于或等于20.5时,我们说体重较重,当![]() 数值小于20.5时,我们说体重较轻,身高大于或等于
数值小于20.5时,我们说体重较轻,身高大于或等于![]() 我们说身高较高,身高小于170cm我们说身高较矮.
我们说身高较高,身高小于170cm我们说身高较矮.
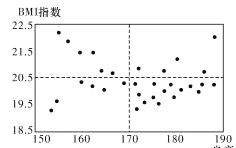
(1)已知某高中共有32名男体育特长生,其身高与![]() 指数的数据如散点图,请根据所得信息,完成下述列联表,并判断是否有
指数的数据如散点图,请根据所得信息,完成下述列联表,并判断是否有![]() 的把握认为男生的身高对
的把握认为男生的身高对![]() 指数有影响.
指数有影响.
身高较矮 | 身高较高 | 合计 | |
体重较轻 | |||
体重较重 | |||
合计 |
(2)①从上述32名男体育特长生中随机选取8名,其身高和体重的数据如表所示:
编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
身高 | 166 | 167 | 160 | 173 | 178 | 169 | 158 | 173 |
体重 | 57 | 58 | 53 | 61 | 66 | 57 | 50 | 66 |
根据最小二乘法的思想与公式求得线性回归方程为![]() .利用已经求得的线性回归方程,请完善下列残差表,并求解释变量(身高)对于预报变量(体重)变化的贡献值(保留两位有效数字)
.利用已经求得的线性回归方程,请完善下列残差表,并求解释变量(身高)对于预报变量(体重)变化的贡献值(保留两位有效数字)![]() ;
;
编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
体重 | 57 | 58 | 53 | 61 | 66 | 57 | 50 | 66 |
残差 | 0.1 | 0.3 | 0.9 |
|
|
②通过残差分析,对于残差的最大(绝对值)的那组数据,需要确认在样本点的采集中是否有人为的错误,已知通过重新采集发现,该组数据的体重应该为![]() .请重新根据最最小二乘法的思想与公式,求出男体育特长生的身高与体重的线性回归方程.
.请重新根据最最小二乘法的思想与公式,求出男体育特长生的身高与体重的线性回归方程.
(参考公式)
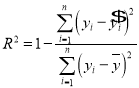 ,
,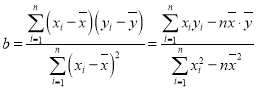 ,
,![]() ,
,![]() ,
,![]() .
.
(参考数据)
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]()
0.10
0.05
0.01
0.005
![]()
2.706
3.811
6.635
7.879
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com