
【题目】我国古代有着辉煌的数学研究成果,其中《周髀算经》、《九章算术》、《海岛算经》、《孙子算经》、《缉古算经》有着丰富多彩的内容,是了解我国古代数学的重要文献.这5部专著中有3部产生于汉、魏、晋、南北朝时期.现拟从这5部专著中选择2部作为学生课外兴趣拓展参考书目,则所选2部专著中至少有一部不是汉、魏、晋、南北朝时期专著的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
科目:高中数学 来源: 题型:
【题目】《中国诗词大会》是由CCTV-10自主研发的一档大型文化益智节目,以“赏中华诗词,寻文化基因品生活之美”为宗旨,带动全民重温经典、从古人的智慧和情怀中汲取营养、涵养心灵,节目广受好评还因为其颇具新意的比赛规则:每场比赛,106位挑战者全部参赛,分为单人追逐赛和擂主争霸赛两部分单人追逐赛的最终优胜者作为攻擂者与守擂擂主进行比拼,竞争该场比赛的擂主,擂主争霸赛以抢答的形式展开,共九道题,抢到并回答正确者得一分,答错则对方得一分,先得五分者获胜,成为本场擂主,比赛结束已知某场擂主争霸赛中,攻擂者与守擂擂主都参与每一次抢题且两人抢到每道题的概率都是![]() ,攻擂者与守擂擂主正确回答每道题的概率分别为
,攻擂者与守擂擂主正确回答每道题的概率分别为![]() ,
,![]() ,且两人各道题是否回答正确均相互独立.
,且两人各道题是否回答正确均相互独立.
(1)比赛开始,求攻擂者率先得一分的概率;
(2)比赛进行中,攻擂者暂时以![]() 领先,设两人共继续抢答了
领先,设两人共继续抢答了![]() 道题比赛结束,求随机变量
道题比赛结束,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国家每年都会对中小学生进行体质健康监测,一分钟跳绳是监测的项目之一.今年某小学对本校六年级300名学生的一分钟跳绳情况做了统计,发现一分钟跳绳个数最低为10,最高为189.现将跳绳个数分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 6组,并绘制出如下的频率分布直方图.
6组,并绘制出如下的频率分布直方图.
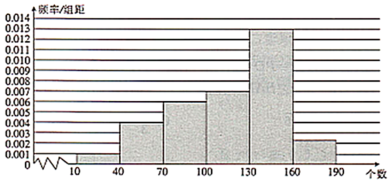
(1)若一分钟跳绳个数达到160为优秀,求该校六年级学生一分钟跳绳为优秀的人数;
(2)上级部门要对该校体质监测情况进行复查,发现每组男、女学生人数比例有很大差别,![]() 组男、女人数之比为
组男、女人数之比为![]() ,
,![]() 组男、女人数之比为
组男、女人数之比为![]() ,
,![]() 组男、女人数之比为
组男、女人数之比为![]() ,
,![]() 组男、女人数之比为
组男、女人数之比为![]() ,
,![]() 组男、女人数之比为
组男、女人数之比为![]() ,
,![]() 组男、女人数之比为
组男、女人数之比为![]() .试估计此校六年级男生一分钟跳绳个数的平均数(同一组中的数据用该组区间的中点值作代表,结果保留整数).
.试估计此校六年级男生一分钟跳绳个数的平均数(同一组中的数据用该组区间的中点值作代表,结果保留整数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为F,过点F,斜率为1的直线与抛物线C交于点A,B,且
的焦点为F,过点F,斜率为1的直线与抛物线C交于点A,B,且![]() .
.
(1)求抛物线C的方程;
(2)过点Q(1,1)作直线交抛物线C于不同于R(1,2)的两点D、E,若直线DR,ER分别交直线![]() 于M,N两点,求|MN|取最小值时直线DE的方程.
于M,N两点,求|MN|取最小值时直线DE的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=eax﹣x﹣1,且f(x)≥0.
(1)求a;
(2)在函数f(x)的图象上取定两点A(x1,f(x1)),B(x2,f(x2))(x1<x2),记直线AB的斜率为k,问:是否存在x0∈(x1,x2),使f'(x0)=k成立?若存在,求出x0的值(用x1,x2表示);若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设正整数m,n满足![]() ,
,![]() ,
,![]() ,
,![]() ,…,
,…,![]() 为集各
为集各![]() 的n元子集,且
的n元子集,且![]() ;
;
(1)若![]() ,满足
,满足![]() ;
;
(i)求证:![]() ;
;
(ii)求满足条件的集合![]() 的个数;
的个数;
(2)若![]() 中至多有一个元素,求证:
中至多有一个元素,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() .
.
(1)若![]() 在区间
在区间![]() 上存在极值,求实数
上存在极值,求实数![]() 的取值范围;
的取值范围;
(2)①设![]() ,求
,求![]() 的最小值;
的最小值;
②定义:对于函数![]() 与
与![]() 定义域上的任意实数
定义域上的任意实数![]() ,若存在常数
,若存在常数![]() ,使得
,使得![]() 和
和![]() 都成立,则称直线
都成立,则称直线![]() 为函数
为函数![]() 与
与![]() 的“隔离直线”.设
的“隔离直线”.设![]() ,试探究
,试探究![]() 与
与![]() 是否存在“隔离直线”?若存在,求出“隔离直线”的方程;若不存在,请说明理由.
是否存在“隔离直线”?若存在,求出“隔离直线”的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年11月5日至10日,首届中国国际进口博览会在国家会展中心(上海)举行,吸引了58个“一带一路”沿线国家的超过1000多家企业参展,成为共建“一带一路”的又一个重要支撑.某企业为了参加这次盛会,提升行业竞争力,加大了科技投入.该企业连续6年来的科技投入![]() (百万元)与收益
(百万元)与收益![]() (百万元)的数据统计如下:
(百万元)的数据统计如下:
科技投入 | 2 | 4 | 6 | 8 | 10 | 12 |
收益 | 5.6 | 6.5 | 12.0 | 27.5 | 80.0 | 129.2 |
并根据数据绘制散点图如图所示:
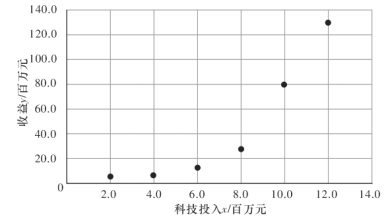
根据散点图的特点,甲认为样本点分布在指数曲线![]() 的周围,据此他对数据进行了一些初步处理.如下表:
的周围,据此他对数据进行了一些初步处理.如下表:
|
|
|
|
|
|
43.5 | 4.5 | 854.0 | 34.7 | 12730.4 | 70 |
其中![]() ,
,![]() .
.
(1)(i)请根据表中数据,建立![]() 关于
关于![]() 的回归方程(保留一位小数);
的回归方程(保留一位小数);
(ii)根据所建立的回归方程,若该企业想在下一年收益达到2亿,则科技投入的费用至少要多少?(其中![]() )
)
(2)乙认为样本点分布在二次曲线![]() 的周围,并计算得回归方程为
的周围,并计算得回归方程为![]() ,以及该回归模型的相关指数
,以及该回归模型的相关指数![]() ,试比较甲乙两人所建立的模型,谁的拟合效果更好.
,试比较甲乙两人所建立的模型,谁的拟合效果更好.
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线方程
,其回归直线方程![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为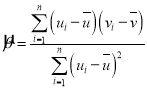 ,
,![]() ,相关指数:
,相关指数: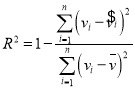 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com