
【题目】设函数![]() .
.
(1)若![]() 在区间
在区间![]() 上存在极值,求实数
上存在极值,求实数![]() 的取值范围;
的取值范围;
(2)①设![]() ,求
,求![]() 的最小值;
的最小值;
②定义:对于函数![]() 与
与![]() 定义域上的任意实数
定义域上的任意实数![]() ,若存在常数
,若存在常数![]() ,使得
,使得![]() 和
和![]() 都成立,则称直线
都成立,则称直线![]() 为函数
为函数![]() 与
与![]() 的“隔离直线”.设
的“隔离直线”.设![]() ,试探究
,试探究![]() 与
与![]() 是否存在“隔离直线”?若存在,求出“隔离直线”的方程;若不存在,请说明理由.
是否存在“隔离直线”?若存在,求出“隔离直线”的方程;若不存在,请说明理由.
【答案】(1)![]() ;(2)①0;②存在,
;(2)①0;②存在,![]()
【解析】
(1)先求导,![]() .再分①
.再分①![]() ,
,![]() ,
, ![]() 三种情况分类讨论.
三种情况分类讨论.
(2)①由![]() ,再求导
,再求导![]() .,分
.,分![]() ,
, ![]() 求解最小值;②由①知
求解最小值;②由①知![]() 与
与![]() 的图象在
的图象在![]() 处有公共点
处有公共点![]() .设
.设![]() 与
与![]() 存在“隔离直线”,方程为
存在“隔离直线”,方程为![]() ,即
,即![]() ,再论证
,再论证![]() 在
在![]() 上恒成立,
上恒成立, ![]() 恒成立即可.
恒成立即可.
(1)![]() .
.
①当![]() 时,
时,![]() ,
,![]() 在区间
在区间![]() 上递增,不存在极值;
上递增,不存在极值;
②当![]() 时,
时,![]() ,
,![]() 在区间
在区间![]() 上递减,不存在极值;
上递减,不存在极值;
③当![]() 时,得
时,得![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,
上单调递增,
在![]() 处取得极小值.
处取得极小值.
综上,实数![]() 的取值范围是
的取值范围是![]() .
.
(2)①![]() ,
,
则![]() .
.
所以当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
因此![]() 时,
时,![]() 取得最小值0;
取得最小值0;
②由①知![]() 与
与![]() 的图象在
的图象在![]() 处有公共点
处有公共点![]() .
.
设![]() 与
与![]() 存在“隔离直线”,方程为
存在“隔离直线”,方程为![]() ,即
,即![]() ,
,
由![]() 在
在![]() 上恒成立,则
上恒成立,则![]() 在
在![]() 上恒成立.
上恒成立.
所以![]() 成立,
成立,
因此![]() .
.
下面证明![]() 恒成立.
恒成立.
设![]() ,则
,则![]() .
.
所以当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
因此![]() 时
时![]() 取得最大值,则
取得最大值,则![]() 恒成立.
恒成立.
故所求“隔离直线”方程为:![]() .
.


科目:高中数学 来源: 题型:
【题目】《孙子算经》是中国古代重要的数学著作,书中有一问题:“今有方物一束,外周一匝有三十二枚,问积几何?”,该著作中提出了一种解决此问题的方法:“重置二位,左位减八,余加右位,至尽虚减一,即得.”通过对该题的研究发现,若一束方物外周一匝的枚数![]() 是8的整数倍时,均可采用此方法求解,如图是解决这类问题的程序框图,若输入
是8的整数倍时,均可采用此方法求解,如图是解决这类问题的程序框图,若输入![]() ,则输出的结果为( )
,则输出的结果为( )
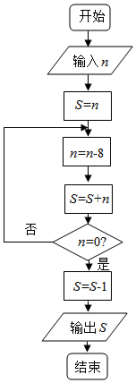
A.80B.47C.79D.48
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代有着辉煌的数学研究成果,其中《周髀算经》、《九章算术》、《海岛算经》、《孙子算经》、《缉古算经》有着丰富多彩的内容,是了解我国古代数学的重要文献.这5部专著中有3部产生于汉、魏、晋、南北朝时期.现拟从这5部专著中选择2部作为学生课外兴趣拓展参考书目,则所选2部专著中至少有一部不是汉、魏、晋、南北朝时期专著的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() ,
,![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的坐标方程为
的坐标方程为![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 相切.
相切.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)在曲线![]() 上取两点
上取两点![]() 、
、![]() 于原点
于原点![]() 构成
构成![]() ,且满足
,且满足![]() ,求面积
,求面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某运动员每次投篮命中的概率都为40%.现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器算出0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果.经随机模拟产生了20组随机数:
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
据此估计,该运动员三次投篮恰有两次命中的概率为( )
A.0.35B.0.25C.0.20D.0.15
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年底,北京2022年冬奥组委会启动志愿者全球招募,仅一个月内报名人数便突破60万,其中青年学生约有50万人.现从这50万青年学生志愿者中,按男女分层抽样随机选取20人进行英语水平测试,所得成绩(单位:分)统计结果用茎叶图记录如下:

(Ⅰ)试估计在这50万青年学生志愿者中,英语测试成绩在80分以上的女生人数;
(Ⅱ)从选出的8名男生中随机抽取2人,记其中测试成绩在70分以上的人数为X,求![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)为便于联络,现将所有的青年学生志愿者随机分成若干组(每组人数不少于5000),并在每组中随机选取![]() 个人作为联络员,要求每组的联络员中至少有1人的英语测试成绩在70分以上的概率大于90%.根据图表中数据,以频率作为概率,给出
个人作为联络员,要求每组的联络员中至少有1人的英语测试成绩在70分以上的概率大于90%.根据图表中数据,以频率作为概率,给出![]() 的最小值.(结论不要求证明)
的最小值.(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的倾斜角为
的倾斜角为![]() ,且经过点
,且经过点![]() .以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,直线
.以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,直线![]() ,从原点O作射线交
,从原点O作射线交![]() 于点M,点N为射线OM上的点,满足
于点M,点N为射线OM上的点,满足![]() ,记点N的轨迹为曲线C.
,记点N的轨迹为曲线C.
(Ⅰ)求出直线![]() 的参数方程和曲线C的直角坐标方程;
的参数方程和曲线C的直角坐标方程;
(Ⅱ)设直线![]() 与曲线C交于P,Q两点,求
与曲线C交于P,Q两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】记![]() 表示m,n中的最大值,如
表示m,n中的最大值,如![]() .已知函数
.已知函数![]() ,
,![]() .
.
(1)设![]() ,求函数
,求函数![]() 在
在![]() 上的零点个数;
上的零点个数;
(2)试探讨是否存在实数![]() ,使得
,使得![]() 对
对![]() 恒成立?若存在,求a的取值范围;若不存在,说明理由.
恒成立?若存在,求a的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() +
+![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为![]() ,直线l:x+2y=4与椭圆有且只有一个交点T.
,直线l:x+2y=4与椭圆有且只有一个交点T.
(I)求椭圆C的方程和点T的坐标;
(Ⅱ)O为坐标原点,与OT平行的直线l′与椭圆C交于不同的两点A,B,直线l′与直线l交于点P,试判断![]() 是否为定值,若是请求出定值,若不是请说明理由.
是否为定值,若是请求出定值,若不是请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com