[题目]是中国古代重要的数学著作.书中有一问题:“今有方物一束.外周一匝有三十二枚.问积几何? .该著作中提出了一种解决此问题的方法:“重置二位.左位减八.余加右位.至尽虚减一.即得. 通过对该题的研究发现.若一束方物外周一匝的枚数是8的整数倍时.均可采用此方法求解.如图是解决这类问题的程序框图.若输入.则输出的结果为( )A.80B.47 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】《孙子算经》是中国古代重要的数学著作，书中有一问题：“今有方物一束，外周一匝有三十二枚，问积几何？”，该著作中提出了一种解决此问题的方法：“重置二位，左位减八，余加右位，至尽虚减一，即得.”通过对该题的研究发现，若一束方物外周一匝的枚数是8的整数倍时，均可采用此方法求解，如图是解决这类问题的程序框图，若输入，则输出的结果为（）

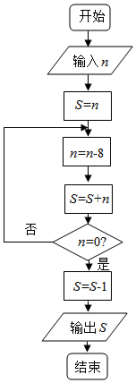
A.80B.47C.79D.48

【答案】C

【解析】

模拟程序的运行，依次写出每次循环得到的，的值，当时，满足条件退出循环，即可得到输出的值．

解：模拟程序的运行，可得

，，

执行循环体，，

不满足条件，执行循环体，，，

满足条件，可得，退出循环，输出的值为；

故选：C．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】在直角坐标系中，直线的参数方程为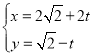（为参数），以为极点，轴的正半轴为极轴建立极坐标系，曲线的极坐标方程为.

（1）求的普通方程和的直角坐标方程；

（2）把曲线向下平移个单位，然后各点横坐标变为原来的倍得到曲线（纵坐标不变），设点是曲线上的一个动点，求它到直线的距离的最小值.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】《中国诗词大会》是由CCTV-10自主研发的一档大型文化益智节目,以“赏中华诗词,寻文化基因品生活之美”为宗旨,带动全民重温经典、从古人的智慧和情怀中汲取营养、涵养心灵,节目广受好评还因为其颇具新意的比赛规则:每场比赛,106位挑战者全部参赛,分为单人追逐赛和擂主争霸赛两部分单人追逐赛的最终优胜者作为攻擂者与守擂擂主进行比拼,竞争该场比赛的擂主,擂主争霸赛以抢答的形式展开,共九道题,抢到并回答正确者得一分,答错则对方得一分,先得五分者获胜,成为本场擂主,比赛结束已知某场擂主争霸赛中,攻擂者与守擂擂主都参与每一次抢题且两人抢到每道题的概率都是,攻擂者与守擂擂主正确回答每道题的概率分别为,,且两人各道题是否回答正确均相互独立.

（1）比赛开始,求攻擂者率先得一分的概率;

（2）比赛进行中,攻擂者暂时以领先,设两人共继续抢答了道题比赛结束,求随机变量的分布列和数学期望.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知椭圆：，离心率，是椭圆的左顶点，是椭圆的左焦点，，直线：.

（1）求椭圆方程；

（2）直线过点与椭圆交于、两点，直线、分别与直线交于、两点，试问：以为直径的圆是否过定点，如果是，请求出定点坐标；如果不是，请说明理由.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某地在每周六的晚上8点到10点半举行灯光展，灯光展涉及到10000盏灯，每盏灯在某一时刻亮灯的概率均为，并且是否亮灯彼此相互独立.现统计了其中100盏灯在一场灯光展中亮灯的时长（单位：），得到下面的频数表：

亮灯时长/
频数	10	20	40	20	10

以样本中100盏灯的平均亮灯时长作为一盏灯的亮灯时长.

（1）试估计的值；

（2）设表示这10000盏灯在某一时刻亮灯的数目.

①求的数学期望和方差；

②若随机变量满足，则认为.假设当时，灯光展处于最佳灯光亮度.试由此估计，在一场灯光展中，处于最佳灯光亮度的时长（结果保留为整数）.

附：

①某盏灯在某一时刻亮灯的概率等于亮灯时长与灯光展总时长的商；

②若，则，，.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知集合A={1，2，3，4，5，6，7，8，9），在集合A中任取三个元素，分别作为一个三位数的个位数，十位数和百位数，记这个三位数为a，现将组成a的三个数字按从小到大排成的三位数记为I（a），按从大到小排成的三位数记为D（a）（例如a=219，则I（a）=129，D（a）=921），阅读如图所示的程序框图，运行相应的程序，任意输入一个a，则输出b的值为（）

A. 792 B. 693 C. 594 D. 495

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】国家每年都会对中小学生进行体质健康监测，一分钟跳绳是监测的项目之一.今年某小学对本校六年级300名学生的一分钟跳绳情况做了统计，发现一分钟跳绳个数最低为10，最高为189.现将跳绳个数分成，，，，，6组，并绘制出如下的频率分布直方图.

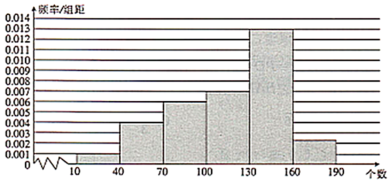
（1）若一分钟跳绳个数达到160为优秀，求该校六年级学生一分钟跳绳为优秀的人数；

（2）上级部门要对该校体质监测情况进行复查，发现每组男、女学生人数比例有很大差别，组男、女人数之比为，组男、女人数之比为，组男、女人数之比为，组男、女人数之比为，组男、女人数之比为，组男、女人数之比为.试估计此校六年级男生一分钟跳绳个数的平均数（同一组中的数据用该组区间的中点值作代表，结果保留整数）.