
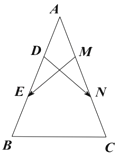
【题目】如图,在等腰△ABC中,AB=AC=3,D,E与M,N分别是AB,AC的三等分点,且![]()
![]() 1,则tanA=_____,
1,则tanA=_____,![]()
![]() _____.
_____.
【答案】![]()
![]() .
.
【解析】
设A(0,b),B(﹣a,0),C(a,0),利用![]()
![]() 1以及
1以及![]() 可求得a,b,在△ABC中利用余弦定理求得
可求得a,b,在△ABC中利用余弦定理求得![]() ,从而可得
,从而可得![]() ;
;![]()
![]() 利用数量积的定义计算.
利用数量积的定义计算.
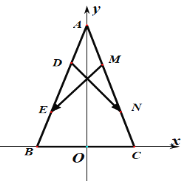
以边BC所在直线为x轴,以边BC的中垂线为y轴,建立如图所示平面直角坐标系,
设A(0,b),B(﹣a,0),C(a,0),且D,E与M,N分别是AB,AC的三等分点,
∴D(![]() ,
,![]() ),E(
),E(![]() ,
,![]() ),M(
),M( ![]() ,
,![]() ),N(
),N( ![]() ,
,![]() ),
),
∴![]() (a,
(a,![]() ),
),![]() (﹣a,
(﹣a,![]() ),且
),且 ![]()
![]() 1,
1,
∴﹣a2![]() 1①,
1①,
又AC=3,∴a2+b2=9②,
联立①②得,a2![]() ,
,
在△ABC中,由余弦定理得,cosA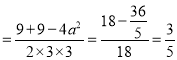 .
.
因为A为等腰三角形的顶角;且cosA![]() ,
,
∴sinA![]() ;
;
∴tanA![]() ;
;
sin![]() ;
;
∴cosB=cos(![]() )=sin
)=sin![]() ;
;
∴![]()
![]()
![]() 3×2a×cosB=﹣3
3×2a×cosB=﹣3![]() .
.
故答案为:(1)![]() ;(2)
;(2)![]() .
.


科目:高中数学 来源: 题型:
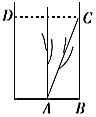
【题目】《九章算术》是我国古代内容极为丰富的数学名著,书中有一个“引葭赴岸”问题:“今有池方一丈,葭生其中央.出水一尺,引葭赴岸,适与岸齐.问水深、葭长各几何?”其意思为“今有水池1丈见方(即![]() 尺),芦苇生长在水的中央,长出水面的部分为1尺.将芦苇向池岸牵引,恰巧与水岸齐接(如图所示).试问水深、芦苇的长度各是多少?假设
尺),芦苇生长在水的中央,长出水面的部分为1尺.将芦苇向池岸牵引,恰巧与水岸齐接(如图所示).试问水深、芦苇的长度各是多少?假设![]() ,现有下述四个结论:
,现有下述四个结论:
①水深为12尺;②芦苇长为15尺;③![]() ;④
;④![]() .
.
其中所有正确结论的编号是( )
A.①③B.①③④C.①④D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,以坐标原点O为极点,x轴正半轴为极轴建立极坐标系。已知曲线C的极坐标方程为![]() ,过点
,过点![]() 的直线l的参数方程为
的直线l的参数方程为 (为参数),直线l与曲线C交于M、N两点。
(为参数),直线l与曲线C交于M、N两点。
(1)写出直线l的普通方程和曲线C的直角坐标方程:
(2)若![]() 成等比数列,求a的值。
成等比数列,求a的值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,左、右顶点分别为
,左、右顶点分别为![]() 、
、![]() ,过左焦点的直线
,过左焦点的直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点(异于
两点(异于![]() 、
、![]() 两点),当直线
两点),当直线![]() 垂直于
垂直于![]() 轴时,四边形
轴时,四边形![]() 的面积为6.
的面积为6.
(1)求椭圆的方程;
(2)设直线![]() 、
、![]() 的交点为
的交点为![]() ;试问
;试问![]() 的横坐标是否为定值?若是,求出定值;若不是,请说明理由.
的横坐标是否为定值?若是,求出定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
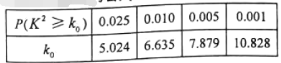
【题目】某单位共有职工2000人,其中男职工1200人,女职工800人为调查2019年“双十一”购物节的消费情况,按照性别采用分层抽样的方法抽取了该单位100人在“双十一”当天网络购物的消费金额(单位:百元),其频率分布直方图如下:

(1)已知抽取的样本中,有3名女职工的消费不低于1000元,现从消费不低于1000元的职工中抽取3名职工进行购物指导,求抽取的3名职工中至少有两名女职工的概率;
(2)在“双十一”当天网络购物消费金额不低于600元者称为“购物狂”,低于600元者称为“理性购物者”.已知在抽取的样本中有18名女职工消费不低于600元,请完成上图中的列联表,并判断能否有99%的把握认为“是不是购物狂”与性别有关.
附:参考数据与公式
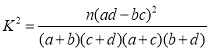
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数学中有许多形状优美、寓意美好的曲线,例如:四叶草曲线就是其中一种,其方程为![]() .给出下列四个结论:
.给出下列四个结论:
①曲线![]() 有四条对称轴;
有四条对称轴;
②曲线![]() 上的点到原点的最大距离为
上的点到原点的最大距离为![]() ;
;
③曲线![]() 第一象限上任意一点作两坐标轴的垂线与两坐标轴围成的矩形面积最大值为
第一象限上任意一点作两坐标轴的垂线与两坐标轴围成的矩形面积最大值为![]() ;
;
④四叶草面积小于![]() .
.
其中,所有正确结论的序号是( )

A.①②B.①③C.①③④D.①②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 分别是
分别是![]() 的边
的边![]() ,
,![]() 上的一点,
上的一点,![]() ,将
,将![]() 沿
沿![]() 折起为
折起为![]() ,使
,使![]() 点位于
点位于![]() 点的位置,连接
点的位置,连接![]() ,
,![]() ,
,![]() .
.
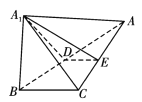
(1)若![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,平面
的中点,平面![]() 与平面
与平面![]() 的交线为
的交线为![]() ,证明:
,证明:![]() ;
;
(2)若平面![]() 平面
平面![]() ,
,![]() 与
与![]() 的面积分别为4和9,
的面积分别为4和9,![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com