
【题目】数学中有许多形状优美、寓意美好的曲线,例如:四叶草曲线就是其中一种,其方程为![]() .给出下列四个结论:
.给出下列四个结论:
①曲线![]() 有四条对称轴;
有四条对称轴;
②曲线![]() 上的点到原点的最大距离为
上的点到原点的最大距离为![]() ;
;
③曲线![]() 第一象限上任意一点作两坐标轴的垂线与两坐标轴围成的矩形面积最大值为
第一象限上任意一点作两坐标轴的垂线与两坐标轴围成的矩形面积最大值为![]() ;
;
④四叶草面积小于![]() .
.
其中,所有正确结论的序号是( )

A.①②B.①③C.①③④D.①②④
【答案】C
【解析】
①利用![]() 之间的代换判断出对称轴的条数;②利用基本不等式求解出到原点的距离最大值;③将面积转化为
之间的代换判断出对称轴的条数;②利用基本不等式求解出到原点的距离最大值;③将面积转化为![]() 的关系式,然后根据基本不等式求解出最大值;④根据
的关系式,然后根据基本不等式求解出最大值;④根据![]() 满足的不等式判断出四叶草与对应圆的关系,从而判断出面积是否小于
满足的不等式判断出四叶草与对应圆的关系,从而判断出面积是否小于![]() .
.
①:当![]() 变为
变为![]() 时,
时, ![]() 不变,所以四叶草图象关于
不变,所以四叶草图象关于![]() 轴对称;
轴对称;
当![]() 变为
变为![]() 时,
时,![]() 不变,所以四叶草图象关于
不变,所以四叶草图象关于![]() 轴对称;
轴对称;
当![]() 变为
变为![]() 时,
时,![]() 不变,所以四叶草图象关于
不变,所以四叶草图象关于![]() 轴对称;
轴对称;
当![]() 变为
变为![]() 时,
时,![]() 不变,所以四叶草图象关于
不变,所以四叶草图象关于![]() 轴对称;
轴对称;
综上可知:有四条对称轴,故正确;
②:因为![]() ,所以
,所以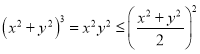 ,
,
所以![]() ,所以
,所以![]() ,取等号时
,取等号时![]() ,
,
所以最大距离为![]() ,故错误;
,故错误;
③:设任意一点![]() ,所以围成的矩形面积为
,所以围成的矩形面积为![]() ,
,
因为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
取等号时![]() ,所以围成矩形面积的最大值为
,所以围成矩形面积的最大值为![]() ,故正确;
,故正确;
④:由②可知![]() ,所以四叶草包含在圆
,所以四叶草包含在圆![]() 的内部,
的内部,
因为圆的面积为:![]() ,所以四叶草的面积小于
,所以四叶草的面积小于![]() ,故正确.
,故正确.
故选:C.


 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案科目:高中数学 来源: 题型:
【题目】某地区现有一个直角梯形水产养殖区ABCD,∠ABC=90°,AB∥CD,AB=800m,BC=1600m,CD=4000m,在点P处有一灯塔(如图),且点P到BC,CD的距离都是1200m,现拟将养殖区ACD分成两块,经过灯塔P增加一道分隔网EF,在△AEF内试验养殖一种新的水产品,当△AEF的面积最小时,对原有水产品养殖的影响最小.设AE=d.
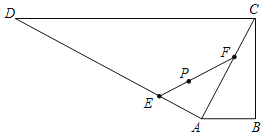
(1)若P是EF的中点,求d的值;
(2)求对原有水产品养殖的影响最小时的d的值,并求△AEF面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() ,离心率
,离心率![]() ,
,![]() 是椭圆的左顶点,
是椭圆的左顶点,![]() 是椭圆的左焦点,
是椭圆的左焦点,![]() ,直线
,直线![]() :
:![]() .
.
(1)求椭圆![]() 方程;
方程;
(2)直线![]() 过点
过点![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点,直线
两点,直线![]() 、
、![]() 分别与直线
分别与直线![]() 交于
交于![]() 、
、![]() 两点,试问:以
两点,试问:以![]() 为直径的圆是否过定点,如果是,请求出定点坐标;如果不是,请说明理由.
为直径的圆是否过定点,如果是,请求出定点坐标;如果不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在边长为4的正方形![]() 中,
中,![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 的中点,现将三角形
的中点,现将三角形![]() 沿
沿![]() 翻折成如图2所示的五棱锥
翻折成如图2所示的五棱锥![]() .
.
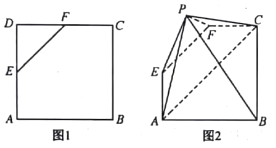
(1)求证:![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={1,2,3,4,5,6,7,8,9),在集合A中任取三个元素,分别作为一个三位数的个位数,十位数和百位数,记这个三位数为a,现将组成a的三个数字按从小到大排成的三位数记为I(a),按从大到小排成的三位数记为D(a)(例如a=219,则I(a)=129,D(a)=921),阅读如图所示的程序框图,运行相应的程序,任意输入一个a,则输出b的值为( )
A. 792 B. 693 C. 594 D. 495
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为原点,极轴为
,以极点为原点,极轴为![]() 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线![]() 过点
过点![]() ,倾斜角为
,倾斜角为![]() .
.
(1)求曲线![]() 的直角坐标方程与直线l的参数方程;
的直角坐标方程与直线l的参数方程;
(2)设直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某搜索引擎广告按照付费价格对搜索结果进行排名,点击一次付费价格排名越靠前,被点击的次数也可能会提高,已知某关键词被甲、乙等多个公司竞争,其中甲、乙付费情况与每小时点击量结果绘制成如下的折线图.
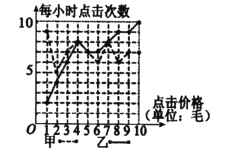
(1)试根据所给数据计算每小时点击次数的均值方差并分析两组数据的特征;
(2)若把乙公司设置的每次点击价格为x,每小时点击次数为y,则点(x,y)近似在一条直线附近.试根据前5次价格与每小时点击次数的关系,求y关于x的回归直线![]() .(附:回归方程系数公式:
.(附:回归方程系数公式: )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com