
【题目】如图1,在边长为4的正方形![]() 中,
中,![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 的中点,现将三角形
的中点,现将三角形![]() 沿
沿![]() 翻折成如图2所示的五棱锥
翻折成如图2所示的五棱锥![]() .
.
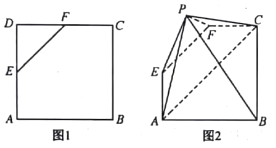
(1)求证:![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点![]() ,
,![]() ,其上顶点到直线
,其上顶点到直线![]() 的距离为2,过点
的距离为2,过点![]() 的直线
的直线![]() 与
与![]() ,
,![]() 轴的交点分别为
轴的交点分别为![]() 、
、![]() ,且
,且![]() .
.
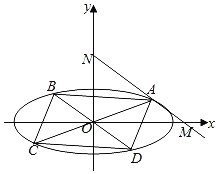
(1)证明:![]() 为定值;
为定值;
(2)如上图所示,若![]() ,
,![]() 关于原点对称,
关于原点对称,![]() ,
,![]() 关于原点对称,且
关于原点对称,且![]() ,求四边形
,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布饼状图,90后从事互联网行业岗位分布条形图,则下列结论中不正确的是( )
注:90后指1990年及以后出生,80后指1980-1989年之间出生,80前指1979年及以前出生.


A.互联网行业从业人员中90后占一半以上
B.互联网行业中从事技术岗位的人数超过总人数的![]()
C.互联网行业中从事运营岗位的人数90后比80前多
D.互联网行业中从事技术岗位的人数90后比80后多
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数学中有许多形状优美、寓意美好的曲线,例如:四叶草曲线就是其中一种,其方程为![]() .给出下列四个结论:
.给出下列四个结论:
①曲线![]() 有四条对称轴;
有四条对称轴;
②曲线![]() 上的点到原点的最大距离为
上的点到原点的最大距离为![]() ;
;
③曲线![]() 第一象限上任意一点作两坐标轴的垂线与两坐标轴围成的矩形面积最大值为
第一象限上任意一点作两坐标轴的垂线与两坐标轴围成的矩形面积最大值为![]() ;
;
④四叶草面积小于![]() .
.
其中,所有正确结论的序号是( )

A.①②B.①③C.①③④D.①②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() (
(![]() )的左焦点为
)的左焦点为![]() ,
,![]() 是
是![]() 上一点,且
上一点,且![]() 与
与![]() 轴垂直,
轴垂直,![]() ,
,![]() 分别为椭圆的右顶点和上顶点,且
分别为椭圆的右顶点和上顶点,且![]() ,且
,且![]() 的面积是
的面积是![]() ,其中
,其中![]() 是坐标原点.
是坐标原点.
(1)求椭圆![]() 的方程.
的方程.
(2)若过点![]() 的直线
的直线![]() ,
,![]() 互相垂直,且分别与椭圆
互相垂直,且分别与椭圆![]() 交于点
交于点![]() ,
,![]() ,
,![]() ,
,![]() 四点,求四边形
四点,求四边形![]() 的面积
的面积![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的左、右焦点为
的左、右焦点为![]() ,
,![]() ,右顶点为
,右顶点为![]() ,上顶点为
,上顶点为![]() .已知
.已知![]() .
.
(Ⅰ)求椭圆的离心率;
(Ⅱ)设![]() 为椭圆上异于其顶点的一点,以线段
为椭圆上异于其顶点的一点,以线段![]() 为直径的圆经过点
为直径的圆经过点![]() ,经过原点的直线
,经过原点的直线![]() 与该圆相切.求直线
与该圆相切.求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为评估两套促销活动方案(方案1运作费用为5元/件;方案2的运作费用为2元件),在某地区部分营销网点进行试点(每个试点网点只采用一种促销活动方案),运作一年后,对比该地区上一年度的销售情况,制作相应的等高条形图如图所示.
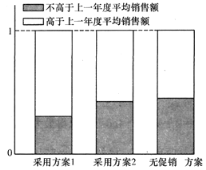
(1)请根据等高条形图提供的信息,为该公司今年选择一套较为有利的促销活动方案(不必说明理由);
(2)已知该公司产品的成本为10元/件(未包括促销活动运作费用),为制定本年度该地区的产品销售价格,统计上一年度的8组售价![]() (单位:元/件,整数)和销量
(单位:元/件,整数)和销量![]() (单位:件)
(单位:件)![]() 如下表所示:
如下表所示:
售价 | 33 | 35 | 37 | 39 | 41 | 43 | 45 | 47 |
销量 | 840 | 800 | 740 | 695 | 640 | 580 | 525 | 460 |
①请根据下列数据计算相应的相关指数![]() ,并根据计算结果,选择合适的回归模型进行拟合;
,并根据计算结果,选择合适的回归模型进行拟合;
②根据所选回归模型,分析售价![]() 定为多少时?利润
定为多少时?利润![]() 可以达到最大.
可以达到最大.
|
|
| |
| 52446.95 | 13142 | 122.89 |
| 124650 | ||
(附:相关指数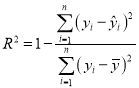 )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com