
分析 (Ⅰ)在已知的数列递推式中取n=1求得数列首项,取n=n-1得另一递推式,两式作差可得an=2an-1-1(n≥2),然后利用构造法可得数列{an-1}是以2为公比的等比数列;
(Ⅱ)由数列{an-1}是以2为公比的等比数列求得an,代入bn=log2(an+1)后求出bn=n,再代入后利用裂项相消法求和.
解答 解:(1)当n=1时,a1=S1=2a1+1,解得a1=-1,
当n>1时,由题意,Sn-1=2an-1+(n-1)
所以,Sn-Sn-1=(2an+n)-[2an-1-(n-1)]=2an-2an-1+1,即an=2an-1-1,
所以 an-1=2(an-1-1),
即 $\frac{{{a_n}-1}}{{{a_{n-1}}-1}}=2$
所以,数列{an-1}是首项为-2,公比为2等比数列;
(2)由上,${a_n}-1=-2•{2^{n-1}}=-{2^n}$,
所以${a_n}=1-{2^n}$,
${b_n}=\frac{1}{{{{log}_2}({1-{a_n}}){{log}_2}({1-{a_{n+1}}})}}=\frac{1}{{{{log}_2}{2^n}•{{log}_2}{2^{n+1}}}}=\frac{1}{{n•({n+1})}}=\frac{1}{n}-\frac{1}{n+1}$,
所以,${T_n}=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+…+\frac{1}{n}-\frac{1}{n+1}=1-\frac{1}{n+1}=\frac{n}{n+1}$.
点评 本题考查了数列递推式,考查了等比关系的确定,训练了裂项相消法求数列的前n项和,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 参加物理竞赛 | 未参加物理竞赛 | |
| 参加数学竞赛 | 9 | 4 |
| 未参加数学竞赛 | 3 | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某小学对五年级的学生进行体质测试,已知五年级一班共有学生30人,测试立定跳远的成绩用茎叶图表示如下(单位:cm):
某小学对五年级的学生进行体质测试,已知五年级一班共有学生30人,测试立定跳远的成绩用茎叶图表示如下(单位:cm):查看答案和解析>>
科目:高中数学 来源: 题型:解答题
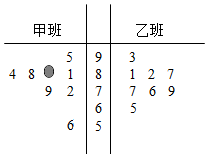 为了解甲、乙两个班级(人数均为60人,入学数学平均分和优秀率都相同,学生勤奋程度 和自觉性都一样)的数学成绩,现随机抽取甲、乙两个班级各8名同学的数学考试成绩,并做出茎叶图,但是不慎污损.已知两个班级所抽取的同学平均成绩相同,回答下面的问题并写出计算过程:
为了解甲、乙两个班级(人数均为60人,入学数学平均分和优秀率都相同,学生勤奋程度 和自觉性都一样)的数学成绩,现随机抽取甲、乙两个班级各8名同学的数学考试成绩,并做出茎叶图,但是不慎污损.已知两个班级所抽取的同学平均成绩相同,回答下面的问题并写出计算过程:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com