
 对某班学生是爱好体育还是爱好文娱进行调查,根据调查得到的数据,所绘制的人数的二维条形图如图.
对某班学生是爱好体育还是爱好文娱进行调查,根据调查得到的数据,所绘制的人数的二维条形图如图.| 男 | 女 | 总计 | |
| 爱好体育 | a | b | a+b |
| 爱好文娱 | c | d | c+d |
| 总计 | a+c | b+d | a+b+c+d |
| p(k2≥k) | 0.5 | 0.4 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
分析 (1)根据图中数据,作出2×2列联表,算出K2与临界值比较,由此得到我们没有足够的把握认为性别与是否更喜欢体育有关系;
(2)确定基本事件的个数,即可求出相应的概率.
解答 解:(1)根据图中数据,作出2×2列联表:
| 更爱好体育 | 更爱好文娱 | 合计 | |
| 男生 | 15 | 10 | 25 |
| 女生 | 5 | 10 | 15 |
| 合计 | 20 | 20 | 40 |
点评 本题考查2×2列联表的作法,考查概率的求法,考查是否可以认为性别与是否爱好体育有关系的判断,是中档题


科目:高中数学 来源: 题型:选择题
| A. | 4$\sqrt{3}$sin(B+60°)+3 | B. | 4$\sqrt{3}$sin(B+30°)+3 | C. | 6sin(B+60°)+3 | D. | 6sin(B+30°)+3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1+$\sqrt{3}$i | B. | -1-$\sqrt{3}$i | C. | $\frac{1}{2}$+$\frac{\sqrt{3}}{2}$i | D. | -$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
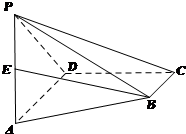 如图,四棱锥P-ABCD的底面是直角梯形,AD∥BC,∠ADC=90°,AD=2BC,PA⊥平面ABCD,E为线段PA的中点.
如图,四棱锥P-ABCD的底面是直角梯形,AD∥BC,∠ADC=90°,AD=2BC,PA⊥平面ABCD,E为线段PA的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com