
分析 (1)求出函数的导数,解关于导函数的不等式,求出函数的单调区间即可;
(2)不存在a,使得函数f(x)在[1,e]上最小值为0,利用函数f(x)的单调增区间为($\frac{1}{a}$,+∞),单调减区间为(0,$\frac{1}{a}$),结合函数的定义域[1,e]进行分类讨论,从而可得结论.
解答 解:(1)f(x)的定义域是(0,+∞),
a=1时,f(x)=lnx+$\frac{1}{x}$,f′(x)=$\frac{x-1}{{x}^{2}}$,
令f′(x)>0,解得:x>1,
令f′(x)<0,解得:0<x<1,
∴f(x)在(0,1)递减,在(1,+∞)递增;
(2)不存在a,使得函数f(x)在[1,e]上最小值为0
由(1)知函数f(x)的单调增区间为($\frac{1}{a}$,+∞),单调减区间为(0,$\frac{1}{a}$)
若1≤$\frac{1}{a}$≤e,即$\frac{1}{e}$≤a≤1,则函数f(x)在[1,e]上最小值为f($\frac{1}{a}$)=-alna+a=0,
∴a=e,不满足题意
若0<$\frac{1}{a}$<1,即a>1,则函数f(x)在[1,e]上最小值为f(1)=1,不满足题意;
若$\frac{1}{a}$>e,0<a<$\frac{1}{e}$时,函数f(x)在[1,e]上最小值为f(e)=a+$\frac{1}{e}$=0,
∴a=-$\frac{1}{e}$,不满足题意.
综上知,不存在a,使得函数f(x)在[1,e]上最小值为0.
点评 本题重点考查导数知识的运用,考查函数的单调性与最值,考查恒成立问题,考查分类讨论的数学思想,综合性强.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 对某班学生是爱好体育还是爱好文娱进行调查,根据调查得到的数据,所绘制的人数的二维条形图如图.
对某班学生是爱好体育还是爱好文娱进行调查,根据调查得到的数据,所绘制的人数的二维条形图如图.| 男 | 女 | 总计 | |
| 爱好体育 | a | b | a+b |
| 爱好文娱 | c | d | c+d |
| 总计 | a+c | b+d | a+b+c+d |
| p(k2≥k) | 0.5 | 0.4 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
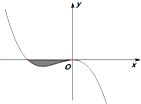 已知函数f(x)=-x3+ax2+bx(a,b∈R)的图象如图所示,它与x轴在原点处相切,且x轴与函数图象所围成区域(图中阴影部分)的面积为$\frac{1}{12}$,若函数f(x)在$({\frac{-1-k}{2},\frac{-1+k}{2}})$上单调增,求k的取值范围.
已知函数f(x)=-x3+ax2+bx(a,b∈R)的图象如图所示,它与x轴在原点处相切,且x轴与函数图象所围成区域(图中阴影部分)的面积为$\frac{1}{12}$,若函数f(x)在$({\frac{-1-k}{2},\frac{-1+k}{2}})$上单调增,求k的取值范围.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
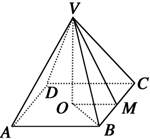 已知四棱锥V-ABCD的底面是面积为16的正方形ABCD,侧面是全等的等腰三角形,一条侧棱长为2$\sqrt{11}$,计算它的高和侧面三角形底边上的高.
已知四棱锥V-ABCD的底面是面积为16的正方形ABCD,侧面是全等的等腰三角形,一条侧棱长为2$\sqrt{11}$,计算它的高和侧面三角形底边上的高.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com