
| A. | 1 | B. | -$\frac{1}{2}$ | C. | -1 | D. | 不确定 |
分析 设出直线方程与抛物线方程联立,求出D,E的纵坐标,利用斜率公式,即可得出结论.
解答 解:设AD的斜率为k,则AE的斜率为-k,D(x1,y1),E(x2,y2),
设AD的方程为y-2=k(x-1),
联立$\left\{\begin{array}{l}{y-2=k(x-1)}\\{{y}^{2}=4x}\end{array}\right.$,消去x、整理得:ky2-4y-4k+8=0,
∴y1=-2+$\frac{4}{k}$,
同理y2=-2-$\frac{4}{k}$,
∴y1+y2=-4,
∴直线DE的斜率为$\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}$=$\frac{4}{{y}_{1}+{y}_{2}}$=-1.
故选:C.
点评 本题是一道直线与抛物线的综合题,考查运算求解能力,注意解题方法的积累,属于中档题.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | 4 | C. | 2$\sqrt{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则在该几何体中,最长的棱的长度是( )
如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则在该几何体中,最长的棱的长度是( )| A. | 4$\sqrt{2}$ | B. | 2$\sqrt{5}$ | C. | 6 | D. | 4$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
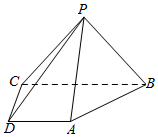 如图,在底面为梯形的四棱锥P-ABCD中,平面PAB⊥平面ABCD,AD∥BC,AD⊥CD,AD=CD=2,BC=4.
如图,在底面为梯形的四棱锥P-ABCD中,平面PAB⊥平面ABCD,AD∥BC,AD⊥CD,AD=CD=2,BC=4.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com