
分析 根据函数f(x)的定义作出函数f(x)的图象,根据函数图象有三个交点,确定三个交点之间的关系即可得到结论.
解答 解:由2$\sqrt{x}$=|x-2|,
平方得4x=x2-4x+4,
即x2-8x+4=0,
解得x=4+2$\sqrt{3}$或x=4-2$\sqrt{3}$,
设x1<x2<x3,
作出函数f(x)的图象如图:
则0<x1<4-2$\sqrt{3}$,x2与x3,关于x=2对称,
则x2+x3=4,
则x1+x2+x3=x1+4,
∵0<x1<4-2$\sqrt{3}$,
∴4<4+x1<8-2$\sqrt{3}$,
即x1+x2+x3的取值范围为$(4,8-2\sqrt{3})$,
故答案为:$(4,8-2\sqrt{3})$
点评 本题主要考查函数与方程的应用,根据定义作出函数的图象,结合函数的对称性是解决本题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2\sqrt{2}$ | B. | $\frac{{3\sqrt{2}}}{2}$ | C. | $\sqrt{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | [1,2] | C. | [-1,1) | D. | (-1,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
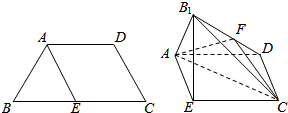 已知四边形ABCD满足AD∥BC,BA=AD=DC=$\frac{1}{2}$BC=a,E是BC的中点,将△BAE沿AE折起到△B1AE的位置,使平面B1AE⊥平面AECD,F为B1D的中点.
已知四边形ABCD满足AD∥BC,BA=AD=DC=$\frac{1}{2}$BC=a,E是BC的中点,将△BAE沿AE折起到△B1AE的位置,使平面B1AE⊥平面AECD,F为B1D的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(2a)<f(3)<f(log2a) | B. | f(3)<f(log2a)<f(2a) | C. | f(log2a)<f(3)<f(2a) | D. | f(log2a)<f(2a)<f(3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{31}{16}$ | B. | $\frac{31}{32}$ | C. | 31 | D. | 15 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com