
【题目】在平面直角坐标系![]() 中,已知抛物线C:
中,已知抛物线C:![]() (
(![]() )的焦点F在直线
)的焦点F在直线![]() 上,平行于x轴的两条直线
上,平行于x轴的两条直线![]() ,
,![]() 分别交抛物线C于A,B两点,交该抛物线的准线于D,E两点.
分别交抛物线C于A,B两点,交该抛物线的准线于D,E两点.

(1)求抛物线C的方程;
(2)若F在线段![]() 上,P是
上,P是![]() 的中点,证明:
的中点,证明:![]() .
.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
(1)根据抛物线的焦点在直线![]() 上,可求得
上,可求得![]() 的值,从而求得抛物线的方程;
的值,从而求得抛物线的方程;
(2)法一:设直线![]() ,
,![]() 的方程分别为
的方程分别为![]() 和
和![]() 且
且![]() ,
,![]() ,
,![]() ,可得
,可得![]() ,
,![]() ,
,![]() ,
,![]() 的坐标,进而可得直线
的坐标,进而可得直线![]() 的方程,根据
的方程,根据![]() 在直线
在直线![]() 上,可得
上,可得![]() ,再分别求得
,再分别求得![]() ,
,![]() ,即可得证;法二:设
,即可得证;法二:设![]() ,
,![]() ,则
,则![]() ,根据直线
,根据直线![]() 的斜率不为0,设出直线
的斜率不为0,设出直线![]() 的方程为
的方程为![]() ,联立直线
,联立直线![]() 和抛物线
和抛物线![]() 的方程,结合韦达定理,分别求出
的方程,结合韦达定理,分别求出![]() ,
,![]() ,化简
,化简![]() ,即可得证.
,即可得证.
(1)抛物线C的焦点![]() 坐标为
坐标为![]() ,且该点在直线
,且该点在直线![]() 上,
上,
所以![]() ,解得
,解得![]() ,故所求抛物线C的方程为
,故所求抛物线C的方程为![]()
(2)法一:由点F在线段![]() 上,可设直线
上,可设直线![]() ,
,![]() 的方程分别为
的方程分别为![]() 和
和![]() 且
且![]() ,
,![]() ,
,![]() ,则
,则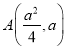 ,
,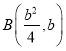 ,
,![]() ,
,![]() .
.
∴直线![]() 的方程为
的方程为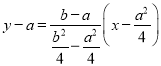 ,即
,即![]() .
.
又点![]() 在线段
在线段![]() 上,∴
上,∴![]() .
.
∵P是![]() 的中点,∴
的中点,∴![]()
∴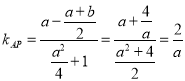 ,
,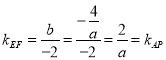 .
.
由于![]() ,
,![]() 不重合,所以
不重合,所以![]()
法二:设![]() ,
,![]() ,则
,则![]()
当直线![]() 的斜率为0时,不符合题意,故可设直线
的斜率为0时,不符合题意,故可设直线![]() 的方程为
的方程为![]()
联立直线![]() 和抛物线
和抛物线![]() 的方程
的方程![]() ,得
,得![]()
又![]() ,
,![]() 为该方程两根,所以
为该方程两根,所以![]() ,
,![]() ,
, ,
,![]() .
.
 ,
,![]()
由于![]() ,
,![]() 不重合,所以
不重合,所以![]()


科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,![]() 底面ABC,
底面ABC,![]() ,H为PC的中点,M为AH的中点
,H为PC的中点,M为AH的中点![]() ,
,![]() .
.
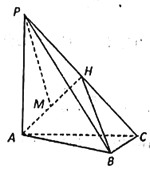
(1)求PM与平面AHB成角的正弦值;
(2)在线段PB上是否存在点N,使得![]() 平面ABC.若存在,请说明点N的位置,若不存在,请说明理由.
平面ABC.若存在,请说明点N的位置,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据有关资料预测,某市下月1—14日的空气质量指数趋势如下图所示.,根据已知折线图,解答下面的问题:
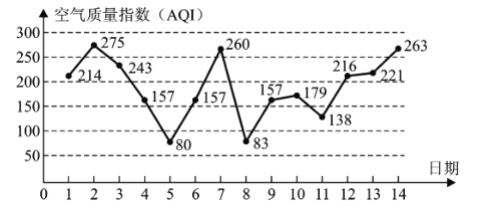
(1)求污染指数的众数及前五天污染指数的平均值;(保留整数)
(2)为了更好发挥空气质量监测服务人民的目的,监测部门在发布空气质量指数的同时,也给出了出行建议,比如空气污染指数大于150时需要戴口罩,超过200时建议减少外出活动等等.如果某人事先没有注意到空气质量预报,而在1—12号这12天中随机选定一天,欲在接下来的两天中(不含选定当天)进行外出活动.求其外出活动的两天期间.
①恰好都遭遇重度及以上污染天气的概率;
②至少有一天能避开重度及以上污染天气的概率.
附:空气质量等级参考表:
|
|
|
|
|
|
|
等级 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在海岸线![]() 一侧有一休闲游乐场,游乐场的前一部分边界为曲线段
一侧有一休闲游乐场,游乐场的前一部分边界为曲线段![]() ,该曲线段是函数
,该曲线段是函数![]() ,
,![]() 的图象,图象的最高点为
的图象,图象的最高点为![]() .边界的中间部分为长1千米的直线段
.边界的中间部分为长1千米的直线段![]() ,且
,且![]() .游乐场的后部分边界是以
.游乐场的后部分边界是以![]() 为圆心的一段圆弧
为圆心的一段圆弧![]() .
.
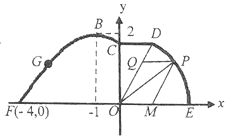
(1)求曲线段![]() 的函数表达式;
的函数表达式;
(2)如图,在扇形![]() 区域内建一个平行四边形休闲区
区域内建一个平行四边形休闲区![]() ,平行四边形的一边在海岸线
,平行四边形的一边在海岸线![]() 上,一边在半径
上,一边在半径![]() 上,另外一个顶点
上,另外一个顶点![]() 在圆弧
在圆弧![]() 上,且
上,且![]() ,求平行四边形休闲区
,求平行四边形休闲区![]() 面积的最大值及此时
面积的最大值及此时![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)求![]() 与
与![]() 的交点的直角坐标;
的交点的直角坐标;
(2)求![]() 上的点到直线
上的点到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解居民的家庭收入情况,某社区组织工作人员从该社区的居民中随机抽取了100户家庭进行问卷调查.经调查发现,这些家庭的月收入在3000元到10000元之间,根据统计数据作出如图所示的频率分布直方图:
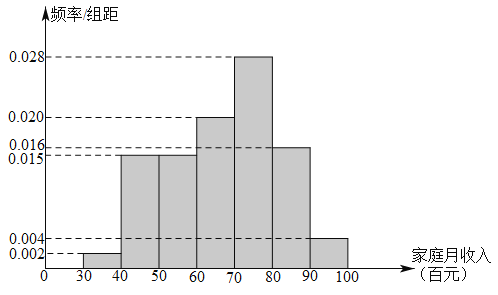
(1)经统计发现,该社区居民的家庭月收入![]() (单位:百元)近似地服从正态分布
(单位:百元)近似地服从正态分布![]() ,其中
,其中![]() 近似为样本平均数.若
近似为样本平均数.若![]() 落在区间
落在区间![]() 的左侧,则可认为该家庭属“收入较低家庭”,社区将联系该家庭,咨询收入过低的原因,并采取相应措施为该家庭提供创收途径.若该社区
的左侧,则可认为该家庭属“收入较低家庭”,社区将联系该家庭,咨询收入过低的原因,并采取相应措施为该家庭提供创收途径.若该社区![]() 家庭月收入为4100元,试判断
家庭月收入为4100元,试判断![]() 家庭是否属于“收入较低家庭”,并说明原因;
家庭是否属于“收入较低家庭”,并说明原因;
(2)将样本的频率视为总体的概率.
①从该社区所有家庭中随机抽取![]() 户家庭,若这
户家庭,若这![]() 户家庭月收入均低于8000元的概率不小于50%,求
户家庭月收入均低于8000元的概率不小于50%,求![]() 的最大值;
的最大值;
②在①的条件下,某生活超市赞助了该社区的这次调查活动,并为这次参与调查的家庭制定了赠送购物卡的活动,赠送方式为:家庭月收入低于![]() 的获赠两次随机购物卡,家庭月收入不低于
的获赠两次随机购物卡,家庭月收入不低于![]() 的获赠一次随机购物卡;每次赠送的购物卡金额及对应的概率分别为:
的获赠一次随机购物卡;每次赠送的购物卡金额及对应的概率分别为:
赠送购物卡金额(单位:元) | 100 | 200 | 300 |
概率 |
|
|
|
则![]() 家庭预期获得的购物卡金额为多少元?(结果保留整数)
家庭预期获得的购物卡金额为多少元?(结果保留整数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com