
分析 (1)利用阶差法可知an=n+4(n≥2),进而验证当n=1时是否成立即可;
(2)由(1)裂项可知cn=$\frac{1}{2}$($\frac{1}{2n-1}$-$\frac{1}{2n+1}$),进而并项相加可知Tn=$\frac{1}{2}$(1-$\frac{1}{2n+1}$),且Tn的最小值为$\frac{1}{3}$,从而问题转化为解不等式$\frac{k}{2017}<\frac{1}{3}$,计算即得结论;
(3)假设存在满足条件的正整数m,分m为奇数、偶数两种情况代入计算即可.
解答 解:(1)因为${S_n}=\frac{1}{2}{n^2}+\frac{9}{2}n,(n∈{N^*})$,
所以an=Sn-Sn-1=n+4(n≥2),
又因为a1=S1=5满足上式,
所以${a_n}=n+4,n∈{N^*}$;
(2)由(1)可知${c_n}=\frac{1}{(2n-1)(2n+1)}$=$\frac{1}{2}$($\frac{1}{2n-1}$-$\frac{1}{2n+1}$),
所以Tn=$\frac{1}{2}$(1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{5}$+…+$\frac{1}{2n-1}$-$\frac{1}{2n+1}$)=$\frac{1}{2}$(1-$\frac{1}{2n+1}$),
显然Tn随着n的增大而增大,故Tn的最小值为$\frac{1}{3}$,
由$\frac{k}{2017}<\frac{1}{3}$可得kmax=672;
(3)结论:不存在满足条件的m.
理由如下:
①当m为奇数时m+15为偶数,则
f(m+15)=5f(m),即3am+15-13=5am,
所以3(m+15+4)-13=5(m+4),解得m=12,矛盾;
②当m为偶数时m+15为奇数,则
f(m+15)=5f(m),即am+15=5(3am-13),
所以m+15+4=5[3(m+4)-13],解得m=$\frac{12}{7}$,矛盾;
综上所述,不存在满足条件的m.
点评 本题考查数列的通项及前n项和,考查分类讨论的思想,考查裂项相消法求和,考查数列的单调性,考查恒成立问题,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:填空题
| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 |
| P(K2≥k) | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 |
| k | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
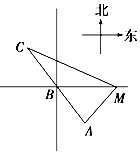 如图所示,已知A、B、C是一条直路上的三点,AB与BC各等于2km,从三点分别遥望塔M,在A处看见塔在北偏东45°方向,在B处看塔在正东方向,在点C处看见塔在南偏东60°方向,则塔M到直路ABC的最短距离为$\frac{14+10\sqrt{3}}{13}$.
如图所示,已知A、B、C是一条直路上的三点,AB与BC各等于2km,从三点分别遥望塔M,在A处看见塔在北偏东45°方向,在B处看塔在正东方向,在点C处看见塔在南偏东60°方向,则塔M到直路ABC的最短距离为$\frac{14+10\sqrt{3}}{13}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com