
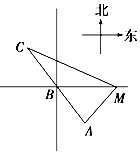
 如图所示,已知A、B、C是一条直路上的三点,AB与BC各等于2km,从三点分别遥望塔M,在A处看见塔在北偏东45°方向,在B处看塔在正东方向,在点C处看见塔在南偏东60°方向,则塔M到直路ABC的最短距离为$\frac{14+10\sqrt{3}}{13}$.
如图所示,已知A、B、C是一条直路上的三点,AB与BC各等于2km,从三点分别遥望塔M,在A处看见塔在北偏东45°方向,在B处看塔在正东方向,在点C处看见塔在南偏东60°方向,则塔M到直路ABC的最短距离为$\frac{14+10\sqrt{3}}{13}$. 分析 根据已知条件求得∠CMA,进而可推断出△MBC与△MBA面积相等,利用三角形面积公式可求得CM和AM的关系,进而在△MAC中利用余弦定理求得a,最后根据三角形面积公式求得答案.
解答 解:已知AB=BC=2,∠AMB=45°,∠CMB=30°,∴∠CMA=75°
易见△MBC与△MBA面积相等,
∴AMsin45°=CMsin30°
即CM=$\sqrt{2}$AM,记AM=a,则CM=$\sqrt{2}$a,
在△MAC中,AC=4,由余弦定理得:16=3a2-2$\sqrt{2}$a2cos75°,
∴a2=$\frac{16}{4-\sqrt{3}}$,记M到AC的距离为h,则$\frac{1}{2}$×$\sqrt{2}$a2sin75°=2h
得h=$\frac{14+10\sqrt{3}}{13}$,
∴塔到直路ABC的最短距离为:$\frac{{14+10\sqrt{3}}}{13}$.
故答案为:$\frac{{14+10\sqrt{3}}}{13}$.
点评 本题主要考查了解三角形的实际应用.考查了学生对基础知识的综合运用.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
 一个封闭立方体的六个面积各标出A,B,C,D,E,F这六个字母,现放成如图所示三种不同的位置,所看见的表面上的字母已标明,则字母A,B,C对面的字母分别是( )
一个封闭立方体的六个面积各标出A,B,C,D,E,F这六个字母,现放成如图所示三种不同的位置,所看见的表面上的字母已标明,则字母A,B,C对面的字母分别是( )| A. | D,E,F | B. | F,D,E | C. | E,F,D | D. | E,D,F |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x0) | B. | -f′(x0) | C. | f′(-x0) | D. | 不一定存在 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m<2或m>4 | B. | -4<m<-2 | C. | 2<m<4 | D. | 以上皆不正确 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com