
某公司拟投资开发某种新能源产品,估计能获得10万元至1000万元的投资收益.为加快开发进程,特制定了产品研制的奖励方案:奖金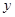 (万元)随投资收益
(万元)随投资收益 (万元)的增加而增加,但奖金总数不超过9万元,同时奖金不超过投资收益的20%.
(万元)的增加而增加,但奖金总数不超过9万元,同时奖金不超过投资收益的20%.
现给出两个奖励模型:①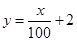 ;②
;②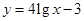 .
.
试分析这两个函数模型是否符合公司要求?
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:高中数学 来源: 题型:解答题
国家助学贷款是由财政贴息的信用贷款(即无利息贷款),旨在帮助高校家庭经济困难学生支付在校学习期间所需的学费、住宿费及生活费.每一年度申请总额不超过6000元.某大学2013届毕业生小王在本科期间共申请了24000元助学贷款,并承诺在毕业后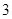 年内(按36个月计)全部还清.签约的单位提供的工资标准为第一年内每月1500元,第
年内(按36个月计)全部还清.签约的单位提供的工资标准为第一年内每月1500元,第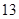 个月开始,每月工资比前一个月增加
个月开始,每月工资比前一个月增加 直到4000元.小王计划前12个月每个月还款额为500,第13个月开始,每月还款额比前一个月多
直到4000元.小王计划前12个月每个月还款额为500,第13个月开始,每月还款额比前一个月多 元.
元.
(1)假设小王在第 个月还清贷款(
个月还清贷款( ),试用
),试用 和
和 表示小王第
表示小王第 (
( )个月的还款额
)个月的还款额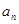 ;
;
(2)当 时,小王将在第几个月还清最后一笔贷款?
时,小王将在第几个月还清最后一笔贷款?
(3)在(2)的条件下,他还清最后一笔贷款的那个月工资的余额是否能满足此月 元的基本生活费?(参考数据:
元的基本生活费?(参考数据: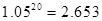 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某面包厂2011年利润为100万元,因市场竞争,若不开发新项目,预测从2012年起每年利润比上一年减少4万元.2012年初,该面包厂一次性投入90万元开发新项目,预测在未扣除开发所投入资金的情况下,第 年(
年( 为正整数,2012年为第一年)的利润为
为正整数,2012年为第一年)的利润为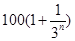 万元.设从2012年起的前
万元.设从2012年起的前 年,该厂不开发新项目的累计利润为
年,该厂不开发新项目的累计利润为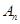 万元,开发新项目的累计利润为
万元,开发新项目的累计利润为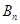 万元(须扣除开发所投入资金).
万元(须扣除开发所投入资金).
(1)求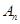 ,
,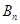 的表达式;
的表达式;
(2)问该新项目的开发是否有效(即开发新项目的累计利润超过不开发新项目的累计利润),如果有效,从第几年开始有效;如果无效,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=ax2+2x+c(a、c∈N*)满足:①f(1)=5;②6<f(2)<11.
(1)求a、c的值;
(2)若对任意的实数x∈ ,都有f(x)-2mx≤1成立,求实数m的取值范围.
,都有f(x)-2mx≤1成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数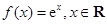 .
.
(Ⅰ) 若直线y=kx+1与f (x)的反函数的图像相切, 求实数k的值;
(Ⅱ) 设x>0, 讨论曲线y=f (x) 与曲线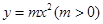 公共点的个数.
公共点的个数.
(Ⅲ) 设a<b, 比较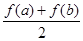 与
与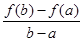 的大小, 并说明理由.
的大小, 并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=lg(ax-bx)(a>1>b>0).
(1)求y=f(x)的定义域;
(2)在函数y=f(x)的图象上是否存在不同的两点,使得过这两点的直线平行于x轴;
(3)当a,b满足什么条件时,f(x)在(1,+∞)上恒取正值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图所示,校园内计划修建一个矩形花坛并在花坛内装置两个相同的喷水器。已知喷水器的喷水区域是半径为5m的圆。问如何设计花坛的尺寸和两个喷水器的位置,才能使花坛的面积最大且能全部喷到水?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com