
已知函数f(x)=lg(ax-bx)(a>1>b>0).
(1)求y=f(x)的定义域;
(2)在函数y=f(x)的图象上是否存在不同的两点,使得过这两点的直线平行于x轴;
(3)当a,b满足什么条件时,f(x)在(1,+∞)上恒取正值.
(1) f(x)的定义域是(0,+∞).
(2)函数y=f(x)的图象上不存在不同两点,使过这两点的直线平行于x轴.
(3)当a≥b+1时,f(x)在(1,+∞)上恒取正值.
解析试题分析:(1)由ax-bx>0得(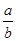 )x>1,
)x>1,
∵a>1>b>0,∴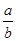 >1,∴x>0.
>1,∴x>0.
∴f(x)的定义域是(0,+∞).
(2)任取x1、x2∈(0,+∞)且x1>x2,
∵a>1>b>0,∴ax1>ax2>1,bx1<bx2<1
∴ax1-bx1>ax2-bx2>0
∴lg(ax1-bx1)>lg(ax2-bx2)
故f(x1)>f(x2)
∴f(x)在(0,+∞)上为增函数.
假设y=f(x)的图象上存在不同的两点A(x1,y1),B(x2,y2),使过A、B两点的直线平行于x轴,则x1≠x2,y1=y2,这与f(x)是增函数矛盾.故函数y=f(x)的图象上不存在不同两点,使过这两点的直线平行于x轴.
(3)∵f(x)是增函数,∴当x∈(1,+∞)时,f(x)>f(1).
这样只需f(1)≥0,即lg(a-b)≥0,
∴a-b≥1.
即当a≥b+1时,f(x)在(1,+∞)上恒取正值.
考点:对数函数的性质,函数的单调性,函数的图象,不等式恒成立问题。
点评:中档题,本题综合性较强,较全面的考查函数的图象和性质。不等式的恒成立问题,往往通过研究函数的单调性及最值,使问题得到解决。本题研究函数的单调性,主要利用了增(减)函数的定义,遵循“设,作差,变形,定号,结论”等加以研究。


科目:高中数学 来源: 题型:解答题
某公司拟投资开发某种新能源产品,估计能获得10万元至1000万元的投资收益.为加快开发进程,特制定了产品研制的奖励方案:奖金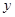 (万元)随投资收益
(万元)随投资收益 (万元)的增加而增加,但奖金总数不超过9万元,同时奖金不超过投资收益的20%.
(万元)的增加而增加,但奖金总数不超过9万元,同时奖金不超过投资收益的20%.
现给出两个奖励模型:①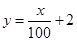 ;②
;②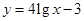 .
.
试分析这两个函数模型是否符合公司要求?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
对于在区间 [ m,n ] 上有意义的两个函数 与
与 ,如果对任意
,如果对任意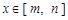 ,均有
,均有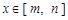 ,则称
,则称 与
与 在 [ m,n ] 上是友好的,否则称
在 [ m,n ] 上是友好的,否则称 与
与 在 [ m,n ]是不友好的.现有两个函数
在 [ m,n ]是不友好的.现有两个函数 与
与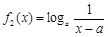 (a > 0且
(a > 0且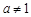 ),给定区间
),给定区间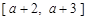 .
.
(1)若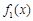 与
与 在给定区间
在给定区间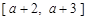 上都有意义,求a的取值范围;
上都有意义,求a的取值范围;
(2)讨论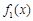 与
与 在给定区间
在给定区间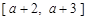 上是否友好.
上是否友好.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了在夏季降温和冬季供暖时减少能源损耗,房屋的房顶和外墙需要建造隔热层,某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元,该建筑物每年的能源消耗费用为C(单位:万元)与隔热层厚度x(单位:cm)满足关系:C(x)=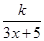 (0
(0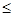 x
x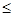 10),若不建隔热层,每年能源消耗费用为8万元。设f(x)为隔热层建造费用与20年的能源消耗费用之和。
10),若不建隔热层,每年能源消耗费用为8万元。设f(x)为隔热层建造费用与20年的能源消耗费用之和。
(1)求k的值及f(x)的表达式;
(2)隔热层修建多厚时,总费用f(x)达到最小,并求最小值。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某商场销售某种商品的经验表明,该商品每日的销售量y(单位:千克)与销售价格x (单位:元/千克)满足关系式y=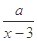 +10(x-6)2,(其中3<x<6,
+10(x-6)2,(其中3<x<6, 为常数,)已知销售价格为5元/千克时,每日可售出该商品11千克。
为常数,)已知销售价格为5元/千克时,每日可售出该商品11千克。
(I)求 的值;
的值;
(II)若该商品的成品为3元/千克,试确定销售价格x的值,使商场每日销售该商品所获得的利润最大。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某连锁分店销售某种商品,每件商品的成本为4元,并且每件商品需向总店交 元(1≤a≤3)的管理费,预计当每件商品的售价为
元(1≤a≤3)的管理费,预计当每件商品的售价为 元(8≤x≤9)时,一年的销售量为(10-x)2万件.
元(8≤x≤9)时,一年的销售量为(10-x)2万件.
(1)求该连锁分店一年的利润L(万元)与每件商品的售价x的函数关系式L(x);
(2)当每件商品的售价为多少元时,该连锁分店一年的利润L最大,并求出L的最
大值M(a).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com