
已知函数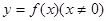 对于任意的
对于任意的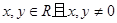 满足
满足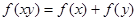 .
.
(1)求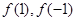 的值;
的值;
(2)求证: 为偶函数;
为偶函数;
(3)若 在
在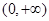 上是增函数,解不等式
上是增函数,解不等式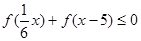
(1)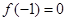 。
。
(2)令 ,得
,得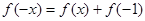 ,可得
,可得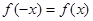 。
。
(3)不等式的解集为:[-1,0)∪(0,2]∪[3,5)∪(5,6]。
解析试题分析:(1)解:∵对于任意的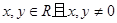 满足
满足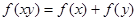
∴令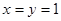 ,得到:
,得到: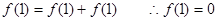
令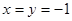 ,得到:
,得到: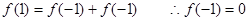 4分
4分
(2)证明:有题可知,令 ,得
,得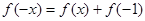
∵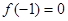 ∴
∴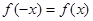 ∴
∴ 为偶函数; 8分
为偶函数; 8分
(3)由(2) 函数 是定义在非零实数集上的偶函数.
是定义在非零实数集上的偶函数.
∴不等式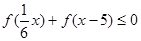 可化为
可化为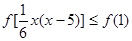
∴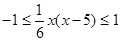 .即:
.即: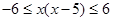 且
且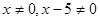
在坐标系内,如图函数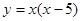 图象与
图象与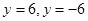 两直线.
两直线.
由图可得x∈[-1,0)∪(0,2]∪[3,5)∪(5,6]
故不等式的解集为:[-1,0)∪(0,2]∪[3,5)∪(5,6] 12分
考点:抽象函数,函数的奇偶性,函数的图象,抽象不等式。
点评:中档题,抽象函数问题,往往利用“赋值法”。抽象不等式问题,往往要利用函数的单调性,结合函数的图象分析得解。


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:解答题
如图,在半径为 、圆心角为
、圆心角为 的扇形的弧上任取一点
的扇形的弧上任取一点 ,作扇形的内接矩形
,作扇形的内接矩形 ,使点
,使点 在
在 上,点
上,点 在
在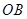 上,设矩形
上,设矩形 的面积为
的面积为 ,
,
(Ⅰ)按下列要求求出函数关系式:
①设 ,将
,将 表示成
表示成 的函数关系式;
的函数关系式;
②设 ,将
,将 表示成
表示成 的函数关系式;
的函数关系式;
(Ⅱ)请你选用(1)中的一个函数关系式,求出 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数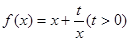 和点
和点 ,过点
,过点 作曲线
作曲线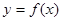 的两条切线
的两条切线 、
、 ,切点分别为
,切点分别为 、
、 .
.
(Ⅰ)设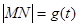 ,试求函数
,试求函数 的表达式;
的表达式;
(Ⅱ)是否存在 ,使得
,使得 、
、 与
与 三点共线.若存在,求出
三点共线.若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(Ⅲ)在(Ⅰ)的条件下,若对任意的正整数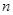 ,在区间
,在区间 内总存在
内总存在 个实数
个实数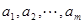 ,
, ,使得不等式
,使得不等式 成立,求
成立,求 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设函数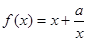 定义域为
定义域为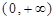 ,且
,且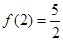 .设点
.设点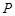 是函数图像上的任意一点,过点
是函数图像上的任意一点,过点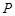 分别作直线
分别作直线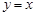 和
和  轴的垂线,垂足分别为
轴的垂线,垂足分别为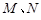 .
.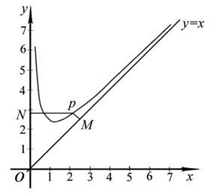
(1)写出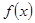 的单调递减区间(不必证明);
的单调递减区间(不必证明);
(2)问: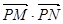 是否为定值?若是,则求出该定值,若不是,则说明理由;
是否为定值?若是,则求出该定值,若不是,则说明理由;
(3)设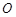 为坐标原点,求四边形
为坐标原点,求四边形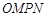 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
随着机构改革工作的深入进行,各单位要减员增效。有一家公司现有职员 人,(
人,( ,且
,且 为偶数),每人每年可创利
为偶数),每人每年可创利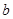 万元。据评估,在经营条件不变的前提下,每裁员1人,则留岗职员每人每年可多创利
万元。据评估,在经营条件不变的前提下,每裁员1人,则留岗职员每人每年可多创利 万元,但公司需支付下岗职员每人每年
万元,但公司需支付下岗职员每人每年 万元的生活费,并且该公司正常运转所需人数不得小于现有员工的
万元的生活费,并且该公司正常运转所需人数不得小于现有员工的 ,为获得最大的经济效益,该公司应裁员多少人?
,为获得最大的经济效益,该公司应裁员多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某公司拟投资开发某种新能源产品,估计能获得10万元至1000万元的投资收益.为加快开发进程,特制定了产品研制的奖励方案:奖金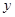 (万元)随投资收益
(万元)随投资收益 (万元)的增加而增加,但奖金总数不超过9万元,同时奖金不超过投资收益的20%.
(万元)的增加而增加,但奖金总数不超过9万元,同时奖金不超过投资收益的20%.
现给出两个奖励模型:①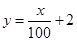 ;②
;②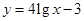 .
.
试分析这两个函数模型是否符合公司要求?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
对于在区间 [ m,n ] 上有意义的两个函数 与
与 ,如果对任意
,如果对任意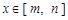 ,均有
,均有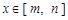 ,则称
,则称 与
与 在 [ m,n ] 上是友好的,否则称
在 [ m,n ] 上是友好的,否则称 与
与 在 [ m,n ]是不友好的.现有两个函数
在 [ m,n ]是不友好的.现有两个函数 与
与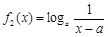 (a > 0且
(a > 0且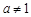 ),给定区间
),给定区间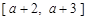 .
.
(1)若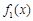 与
与 在给定区间
在给定区间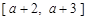 上都有意义,求a的取值范围;
上都有意义,求a的取值范围;
(2)讨论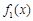 与
与 在给定区间
在给定区间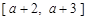 上是否友好.
上是否友好.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某商场销售某种商品的经验表明,该商品每日的销售量y(单位:千克)与销售价格x (单位:元/千克)满足关系式y=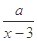 +10(x-6)2,(其中3<x<6,
+10(x-6)2,(其中3<x<6, 为常数,)已知销售价格为5元/千克时,每日可售出该商品11千克。
为常数,)已知销售价格为5元/千克时,每日可售出该商品11千克。
(I)求 的值;
的值;
(II)若该商品的成品为3元/千克,试确定销售价格x的值,使商场每日销售该商品所获得的利润最大。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com