
随着机构改革工作的深入进行,各单位要减员增效。有一家公司现有职员 人,(
人,( ,且
,且 为偶数),每人每年可创利
为偶数),每人每年可创利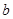 万元。据评估,在经营条件不变的前提下,每裁员1人,则留岗职员每人每年可多创利
万元。据评估,在经营条件不变的前提下,每裁员1人,则留岗职员每人每年可多创利 万元,但公司需支付下岗职员每人每年
万元,但公司需支付下岗职员每人每年 万元的生活费,并且该公司正常运转所需人数不得小于现有员工的
万元的生活费,并且该公司正常运转所需人数不得小于现有员工的 ,为获得最大的经济效益,该公司应裁员多少人?
,为获得最大的经济效益,该公司应裁员多少人?
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:高中数学 来源: 题型:解答题
“活水围网”养鱼技术具有养殖密度高、经济效益好的特点.研究表明:“活水围网”养鱼时,某种鱼在一定的条件下,每尾鱼的平均生长速度 (单位:千克/年)是养殖密度
(单位:千克/年)是养殖密度 (单位:尾/立方米)的函数.当
(单位:尾/立方米)的函数.当 不超过4(尾/立方米)时,
不超过4(尾/立方米)时, 的值为
的值为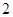 (千克/年);当
(千克/年);当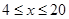 时,
时, 是
是 的一次函数;当
的一次函数;当 达到
达到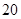 (尾/立方米)时,因缺氧等原因,
(尾/立方米)时,因缺氧等原因, 的值为
的值为 (千克/年).
(千克/年).
(1)当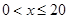 时,求函数
时,求函数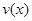 的表达式;
的表达式;
(2)当养殖密度 为多大时,鱼的年生长量(单位:千克/立方米)
为多大时,鱼的年生长量(单位:千克/立方米)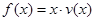 可以达到最大,并求出最大值.
可以达到最大,并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=ax2+2x+c(a、c∈N*)满足:①f(1)=5;②6<f(2)<11.
(1)求a、c的值;
(2)若对任意的实数x∈ ,都有f(x)-2mx≤1成立,求实数m的取值范围.
,都有f(x)-2mx≤1成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数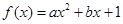 (
(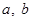 为实数,
为实数,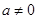 ,
,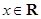 ),
),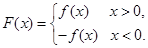
(Ⅰ)若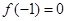 ,且函数
,且函数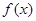 的值域为
的值域为 ,求
,求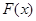 的表达式;
的表达式;
(Ⅱ)在(Ⅰ)的条件下,当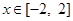 时,
时, 是单调函数,求实数
是单调函数,求实数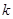 的取值范围;
的取值范围;
(Ⅲ)设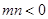 ,
,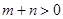 ,
,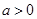 ,且函数
,且函数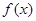 为偶函数,判断
为偶函数,判断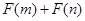 是否大于
是否大于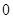 ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
江苏某地区要建造一条防洪堤,其横断面为等腰梯形,腰与底边成角为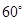 (如图),考虑到防洪堤坚固性及石块用料等因素,设计其横断面要求面积为
(如图),考虑到防洪堤坚固性及石块用料等因素,设计其横断面要求面积为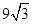 平方米,且高度不低于
平方米,且高度不低于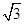 米,设防洪堤横断面的腰长为
米,设防洪堤横断面的腰长为 米,外周长(梯形的上底线段BC与两腰长的和)为
米,外周长(梯形的上底线段BC与两腰长的和)为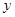 米.
米.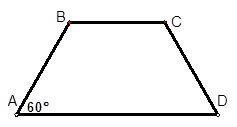
(1)求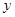 关于
关于 的函数关系式,并指出其定义域;
的函数关系式,并指出其定义域;
(2)要使防洪提的横断面的外周长不超过10.5米,则其腰长应在什么范围内?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com