
”¾ĢāÄæ”æĄ¼Ģģ¹ŗĪļ¹ć³”ijÓŖĻś²æĆÅĖ껜³é²éĮĖ100ĆūŹŠĆńŌŚ2018Äź¹śĒģ³¤¼ŁĘŚ¼ä¹ŗĪļ¹ć³”µÄĻū·Ń½š¶ī£¬ĖłµĆŹż¾ŻČē±ķ£¬ŅŃÖŖĻū·Ń½š¶ī²»³¬¹ż3Ē§ŌŖÓė³¬¹ż3Ē§ŌŖµÄČĖŹż±ČĒ”ĪŖ![]() .
.
Ļū·Ń½š¶ī£Øµ„Ī»£ŗĒ§ŌŖ£© | ČĖŹż | ʵĀŹ |
| 8 | 0.08 |
| 12 | 0.12 |
|
|
|
|
|
|
| 8 | 0.08 |
| 7 | 0.07 |
ŗĻ¼Ę | 100 | 1.00 |

£Ø1£©ŹŌČ·¶Ø![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() µÄÖµ£¬²¢²¹Č«ĘµĀŹ·Ö²¼Ö±·½Ķ¼£ØČēĶ¼£©£»
µÄÖµ£¬²¢²¹Č«ĘµĀŹ·Ö²¼Ö±·½Ķ¼£ØČēĶ¼£©£»
£Ø2£©ÓĆ·Ö²ć³éŃłµÄ·½·Ø“ÓĻū·Ń½š¶īŌŚ![]() ”¢
”¢![]() ŗĶ
ŗĶ![]() µÄČżøöČŗĢåÖŠ³éČ”7ČĖ½ųŠŠĪŹ¾ķµ÷²é£¬Ōņø÷Š”×éÓ¦³éČ”¼øČĖ£æČō“ÓÕā7ČĖÖŠĖ껜єȔ2ČĖ£¬Ōņ“Ė2ČĖĄ“×ŌĶ¬Ņ»ČŗĢåµÄøÅĀŹŹĒ¶ąÉŁ£æ
µÄČżøöČŗĢåÖŠ³éČ”7ČĖ½ųŠŠĪŹ¾ķµ÷²é£¬Ōņø÷Š”×éÓ¦³éČ”¼øČĖ£æČō“ÓÕā7ČĖÖŠĖ껜єȔ2ČĖ£¬Ōņ“Ė2ČĖĄ“×ŌĶ¬Ņ»ČŗĢåµÄøÅĀŹŹĒ¶ąÉŁ£æ
”¾“š°ø”æ£Ø1£©¼ū½āĪö£Ø2£©2£¬3£¬2£»![]()
”¾½āĪö”æ
(1)ÓÉĢāŅāŹ×ĻČĮŠ·½³ĢĒóµĆx,yµÄÖµ£¬Č»ŗóÓÉøÅĀŹ¹«Ź½æɵĆp,qµÄÖµ£¬×īŗó»ęÖĘʵĀŹ·Ö²¼Ö±·½Ķ¼¼“æÉ£»
(2)Ź×ĻČČ·¶ØĖłŠč³éČ”µÄČĖŹż£¬Č»ŗóĮŠ³öĖłÓŠæÉÄܵĽį¹ū£¬½įŗĻ¹ÅµäøÅŠĶ¼ĘĖć¹«Ź½æɵĆĀś×ćĢāŅāµÄøÅĀŹÖµ.
£Ø1£©øł¾ŻĢāŅā£¬ÓŠ £¬
£¬
½āµĆ![]() .
.
”ą![]() £¬
£¬![]() £®
£®
²¹Č«ĘµĀŹ·Ö²¼Ö±·½Ķ¼ČēĶ¼ĖłŹ¾£ŗ

£Ø2£©øł¾ŻĢāŅā£¬Ļū·Ń½š¶īŌŚ![]() ÄŚµÄČĖŹżĪŖ
ÄŚµÄČĖŹżĪŖ![]() £ØČĖ£©£¬¼ĒĪŖ
£ØČĖ£©£¬¼ĒĪŖ![]() £¬
£¬![]() £¬
£¬
Ļū·Ń½š¶īŌŚ![]() ÄŚµÄČĖŹżĪŖ
ÄŚµÄČĖŹżĪŖ![]() £ØČĖ£©£¬¼ĒĪŖ1£¬2£¬3£®””
£ØČĖ£©£¬¼ĒĪŖ1£¬2£¬3£®””
Ļū·Ń½š¶īŌŚ![]() ÄŚµÄČĖŹżĪŖ
ÄŚµÄČĖŹżĪŖ![]() £ØČĖ£©£¬¼ĒĪŖ
£ØČĖ£©£¬¼ĒĪŖ![]() £¬
£¬![]() £®
£®
Ōņ“ÓÕā7ČĖÖŠĖ껜єȔ2ČĖµÄĖłÓŠµÄ»ł±¾ŹĀ¼žĪŖ£ŗ![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬¹²21ÖÖ£¬
£¬¹²21ÖÖ£¬
Éč”°2ČĖĄ“×ŌĶ¬Ņ»ČŗĢå”±ĪŖŹĀ¼ž![]() £¬ŌņŹĀ¼ž
£¬ŌņŹĀ¼ž![]() °üŗ¬µÄ»ł±¾ŹĀ¼žÓŠ
°üŗ¬µÄ»ł±¾ŹĀ¼žÓŠ![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬¹²5ÖÖ£¬
£¬¹²5ÖÖ£¬
ÓɹŵäøÅŠĶøÅĀŹ¹«Ź½µĆ![]() £®
£®
ĖłŅŌ“Ė2ČĖĄ“×ŌĶ¬Ņ»ČŗĢåµÄøÅĀŹŹĒ![]() .
.



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖĶÖŌ²![]() £¬¶ŌÓŚČĪŅāŹµŹż
£¬¶ŌÓŚČĪŅāŹµŹż![]() £¬ĶÖŌ²±»ĻĀĮŠÖ±ĻßĖł½ŲµĆµÄĻŅ³¤Óė±»Ö±Ļß
£¬ĶÖŌ²±»ĻĀĮŠÖ±ĻßĖł½ŲµĆµÄĻŅ³¤Óė±»Ö±Ļß![]() Ėł½ŲµĆµÄĻŅ³¤²»æÉÄÜĻąµČµÄŹĒ£Ø £©
Ėł½ŲµĆµÄĻŅ³¤²»æÉÄÜĻąµČµÄŹĒ£Ø £©
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÉ菿ĮŠ![]() µÄĶØĻī¹«Ź½ĪŖ
µÄĶØĻī¹«Ź½ĪŖ![]() £Ø
£Ø![]() £¬
£¬ ![]() £©£¬ŹżĮŠ
£©£¬ŹżĮŠ![]() ¶ØŅåČēĻĀ£ŗ¶ŌÓŚÕżÕūŹż
¶ØŅåČēĻĀ£ŗ¶ŌÓŚÕżÕūŹż![]() £¬
£¬ ![]() ŹĒŹ¹µĆ²»µČŹ½
ŹĒŹ¹µĆ²»µČŹ½![]() ³ÉĮ¢µÄĖłÓŠ
³ÉĮ¢µÄĖłÓŠ![]() ÖŠµÄ×īŠ”Öµ.
ÖŠµÄ×īŠ”Öµ.
£Ø1£©Čō![]() £¬
£¬ ![]() £¬Ēó
£¬Ēó![]() £»
£»
£Ø2£©Čō![]() £¬
£¬ ![]() £¬ĒóŹżĮŠ
£¬ĒóŹżĮŠ![]() µÄĒ°
µÄĒ°![]() ĻīŗĶ¹«Ź½£»
ĻīŗĶ¹«Ź½£»
£Ø3£©ŹĒ·ń“ęŌŚ![]() ŗĶ
ŗĶ![]() £¬Ź¹µĆ
£¬Ź¹µĆ![]()
![]() £æČē¹ū“ęŌŚ£¬Ēó
£æČē¹ū“ęŌŚ£¬Ēó![]() ŗĶ
ŗĶ![]() µÄȔֵ·¶Ī§£»Čē¹ū²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ.
µÄȔֵ·¶Ī§£»Čē¹ū²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ£Ø1£©ŅŃÖŖÉČŠĪµÄÖܳ¤ĪŖ8£¬Ć껿ŹĒ4£¬ĒóÉČŠĪµÄŌ²ŠÄ½Ē£®
£Ø2£©ŅŃÖŖÉČŠĪµÄÖܳ¤ĪŖ40£¬µ±ĖüµÄ°ė¾¶ŗĶŌ²ŠÄ½ĒČ”ŗĪÖµŹ±£¬²ÅŹ¹ÉČŠĪµÄĆ껿×ī“ó£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖŗÆŹżf£Øx£©= 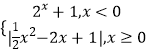 £¬·½³Ģf2£Øx£©©af£Øx£©+b=0£Øb”Ł0£©ÓŠĮłøö²»Ķ¬µÄŹµŹż½ā£¬Ōņ3a+bµÄȔֵ·¶Ī§ŹĒ£Ø £©
£¬·½³Ģf2£Øx£©©af£Øx£©+b=0£Øb”Ł0£©ÓŠĮłøö²»Ķ¬µÄŹµŹż½ā£¬Ōņ3a+bµÄȔֵ·¶Ī§ŹĒ£Ø £©
A.[6£¬11]
B.[3£¬11]
C.£Ø6£¬11£©
D.£Ø3£¬11£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijĶ¬Ń§ŌŚŃŠ¾æѧĻ°ÖŠ£¬ŹÕ¼Æµ½Ä³ÖĘŅ©³§½ńÄź5øöŌĀ¼×½ŗÄŅÉś²ś²śĮæ£Øµ„Ī»£ŗĶņŗŠ£©µÄŹż¾ŻČēĻĀ±ķĖłŹ¾£ŗ
| 1 | 2 | 3 | 4 | 5 |
| 5 | 5 | 6 | 6 | 8 |
Čō![]() ĻߊŌĻą¹Ų£¬ĻߊŌ»Ų¹é·½³ĢĪŖ
ĻߊŌĻą¹Ų£¬ĻߊŌ»Ų¹é·½³ĢĪŖ![]() £¬ŌņŅŌĻĀĪŖÕęĆüĢāµÄŹĒ£Ø £©
£¬ŌņŅŌĻĀĪŖÕęĆüĢāµÄŹĒ£Ø £©
A. ![]() ĆæŌö¼Ó1øöµ„Ī»³¤¶Č£¬Ōņ
ĆæŌö¼Ó1øöµ„Ī»³¤¶Č£¬Ōņ![]() Ņ»¶ØŌö¼Ó0.7øöµ„Ī»³¤¶Č
Ņ»¶ØŌö¼Ó0.7øöµ„Ī»³¤¶Č
B. ![]() ĆæŌö¼Ó1øöµ„Ī»³¤¶Č£¬Ōņ
ĆæŌö¼Ó1øöµ„Ī»³¤¶Č£¬Ōņ![]() ±Ų¼õÉŁ0.7øöµ„Ī»³¤¶Č
±Ų¼õÉŁ0.7øöµ„Ī»³¤¶Č
C. µ±![]() Ź±£¬
Ź±£¬![]() µÄŌ¤²āÖµĪŖ8.1ĶņŗŠ
µÄŌ¤²āÖµĪŖ8.1ĶņŗŠ
D. ĻߊŌ»Ų¹éÖ±Ļß![]() ¾¹żµć
¾¹żµć![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖĶÖŌ²![]()
![]() µÄ×ó½¹µć
µÄ×ó½¹µć![]() ×󶄵ć
×󶄵ć![]() .
.
£Ø¢ń£©ĒóĶÖŌ²![]() µÄ·½³Ģ£»
µÄ·½³Ģ£»
£Ø¢ņ£©ŅŃÖŖ![]() £¬
£¬![]() ŹĒĶÖŌ²ÉĻµÄĮ½µć£¬
ŹĒĶÖŌ²ÉĻµÄĮ½µć£¬![]() ŹĒĶÖŌ²ÉĻĪ»ÓŚÖ±Ļß
ŹĒĶÖŌ²ÉĻĪ»ÓŚÖ±Ļß![]() Į½²ąµÄ¶Æµć.Čō
Į½²ąµÄ¶Æµć.Čō![]() £¬ŹŌĪŹÖ±Ļß
£¬ŹŌĪŹÖ±Ļß![]() µÄŠ±ĀŹŹĒ·ńĪŖ¶ØÖµ£æĒėĖµĆ÷ĄķÓÉ.
µÄŠ±ĀŹŹĒ·ńĪŖ¶ØÖµ£æĒėĖµĆ÷ĄķÓÉ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖŗÆŹż![]() £Ø
£Ø![]() £©.
£©.
£Ø1£©µ±![]() Ź±£¬ĒóĒśĻß
Ź±£¬ĒóĒśĻß![]() ŌŚµć
ŌŚµć![]() “¦µÄĒŠĻß·½³Ģ£»
“¦µÄĒŠĻß·½³Ģ£»
£Ø2£©ĒóŗÆŹż![]() µÄµ„µ÷Ēų¼ä£»
µÄµ„µ÷Ēų¼ä£»
£Ø3£©Čō¶Ō![]() £Ø
£Ø![]() ĪŖ×ŌČ»¶ŌŹżµÄµ×Źż£©£¬
ĪŖ×ŌČ»¶ŌŹżµÄµ×Źż£©£¬![]() ŗć³ÉĮ¢£¬Ē󏵏ż
ŗć³ÉĮ¢£¬Ē󏵏ż![]() µÄȔֵ·¶Ī§.
µÄȔֵ·¶Ī§.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚÖ±½ĒĢŻŠĪABCDÖŠ£¬AD”ĪBC, AB”ĶBC, BD”ĶDC£¬µćEŹĒBC±ßµÄÖŠµć£¬½«”÷ABDŃŲBDÕŪĘš£¬Ź¹Ę½ĆęABD”ĶĘ½ĆęBCD£¬Į¬½ÓAE, AC, DE,µĆµ½ČēĶ¼ĖłŹ¾µÄæÕ¼ä¼øŗĪĢ壮
 ””””
””””
(1)ĒóÖ¤£ŗAB”ĶĘ½ĆęADC£»
(2)ČōAD£½1£¬AB£½![]() £¬ĒóµćBµ½Ę½ĆęADEµÄ¾ąĄė£®
£¬ĒóµćBµ½Ę½ĆęADEµÄ¾ąĄė£®
²éæ““š°øŗĶ½āĪö>>
¹ś¼ŹŃ§Š£ÓÅŃ” - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com