练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知圆：内有一点，过点作直线交圆于、两点．

    （1）当经过圆心时，求直线的方程；

    （2）当弦被点平分时，写出直线的方程；

    （3）当直线的倾斜角为时，求弦的长．

    【答案】（1） ；（2） ；（3）.

    【解析】

    试题分析：（1）求出圆的圆心，代入直线的方程，求出直线的斜率，即可求出直线的方程；（2）当弦被点平分时，求出直线的斜率，即可写出直线的方程；（3）当直线的倾斜角为时，求出直线的斜率，然后求出直线的方程，利用点到直线的距离，半径，半弦长的关系求弦的长.

    试题解析：（1）已知圆：的圆心为，因直线过点、，所以直线的斜率为，直线的方程为，即．

    （2）当弦被点平分时，，直线的方程为，即．

    （3）当直线的倾斜角为时，斜率为，直线的方程为，即，圆心到直线的距离为，圆的半径为，弦的长为．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某班倡议假期每位学生至少阅读一本名著，为了解学生的阅读情况，对该班所有学生进行了调查．调查结果如下表：

    阅读名著的本数

    1

    2

    3

    4

    5

    男生人数

    3

    1

    2

    1

    3

    女生人数

    1

    3

    3

    1

    2

    （1）试根据上述数据，求这个班级女生阅读名著的平均本数；

    （2）若从阅读本名著的学生中任选人交流读书心得，求选到男生和女生各人的概率；

    （3）试比较该班男生阅读名著本数的方差与女生阅读名著本数的方差的大小（只需写出结论）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （Ⅰ）当时，求的极值；

    （Ⅱ）若曲线在点处切线的斜率为3，且对任意都成立，求整数的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

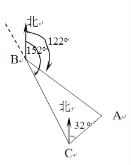
    【题目】如图，货轮在海上以35n mile/h的速度沿方位角（从正北方向顺时针转到目标方向线的水平角）为的方向航行．为了确定船位，在B点处观测到灯塔A的方位角为．半小时后，货轮到达C点处，观测到灯塔A的方位角为．求此时货轮与灯塔之间的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】对定义在区间上的函数和，如果对任意，都有成立，那么称函数在区间上可被替代，称为“替代区间”．给出以下问题：

    ①在区间上可被替代；

    ②可被替代的一个“替代区间”为；

    ③在区间可被替代，则；

    ④（），（），则存在实数（），使得在区间上被替代； 其中真命题有 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）若对，不等式恒成立，求实数的取值范围；

    （2）记，那么当时，是否存在区间使得函数在区间上的值域恰好为？若存在，请求出区间；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】对于函数，若在定义域内存在实数满足，则称为“局部奇函数”.

    为定义在上的“局部奇函数”；

    方程有两个不等实根；

    若“”为假命题，“”为真命题，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（10分）如图所示，在三棱锥中，底面，，，，动点D在线段AB 上．

    （1）求证：平面⊥平面；

    （2）当时，求三棱锥的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在12件同类型的零件中有2件次品，抽取3次进行检验，每次抽取1件，并且取出后不再放回，若以ξ和η分别表示取到的次品数和正品数．

    （1）求ξ的分布列、均值和方差；

    （2）求η的分布列、均值和方差．

    查看答案和解析>>

    同步练习册答案