
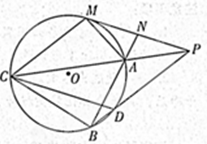
如图,已知圆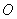 外有一点
外有一点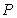 ,作圆
,作圆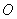 的切线
的切线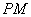 ,
,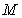 为切点,过
为切点,过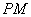 的中点
的中点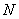 ,作割线
,作割线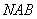 ,交圆于
,交圆于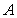 、
、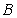 两点,连接
两点,连接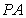 并延长,交圆
并延长,交圆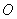 于点
于点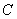 ,连续
,连续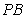 交圆
交圆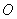 于点
于点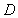 ,若
,若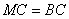 .
.
(1)求证:△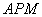 ∽△
∽△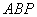 ;
;
(2)求证:四边形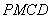 是平行四边形.
是平行四边形.
(1)由切割线定理,及N是PM的中点,可得PN2=NA•NB,结合∠PNA=∠BNP,可得△PNA∽△BNP,则∠APN=∠PBN,即∠APM=∠PBA;再由MC=BC,可得∠MAC=∠BAC,再由等角的补角相等可得∠MAP=∠PAB,进而得到△APM∽△ABP
(2)由∠ACD=∠PBN,可得∠PCD=∠CPM,即PM∥CD;由△APM∽△ABP,PM是圆O的切线,可证得∠MCP=∠DPC,即MC∥PD;再由平行四边形的判定定理得到四边形PMCD是平行四边形.
解析试题分析:证明:(Ⅰ)∵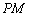 是圆
是圆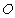 的切线,
的切线,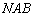 是圆
是圆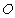 的割线,
的割线,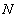 是
是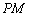 的中点,证明:(Ⅰ)∵PM是圆O的切线,NAB是圆O的割线,N是PM的中点,∴MN2=PN2=NA•NB,又∵∠PNA=∠BNP,
的中点,证明:(Ⅰ)∵PM是圆O的切线,NAB是圆O的割线,N是PM的中点,∴MN2=PN2=NA•NB,又∵∠PNA=∠BNP,
∴△PNA∽△BNP,∴∠APN=∠PBN,即∠APM=∠PBA,.∵MC=BC,
∴∠MAC=∠BAC,∴∠MAP=∠PAB,∴△APM∽△ABP…(5分)
(Ⅱ)∵∠ACD=∠PBN,
∴∠ACD=∠PBN=∠APN,即∠PCD=∠CPM,
∴PM∥CD.∵△APM∽△ABP,∴∠PMA=∠BPA∵PM是圆O的切线,∴∠PMA=∠MCP,∴∠PMA=∠BPA=∠MCP,即∠MCP=∠DPC,∴MC∥PD,∴四边形PMCD是平行四边形.…(10分)
考点:切割线定理,圆周角定理
点评:本题考查的知识点是切割线定理,圆周角定理,三角形相似的判定与性质,平行四边形的判定,熟练掌握平面几何的基本定理是解答本题的关键.


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:高中数学 来源: 题型:解答题
如图,已知圆⊙O1与圆⊙O2外切于点P,过点P的直线交圆⊙O1于A,交圆⊙O2于B,AC为圆⊙O1直径,BD与⊙O2相切于B,交AC延长线于D.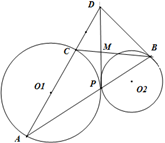
(Ⅰ)求证: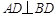
(Ⅱ)若BC、PD相交于点M,则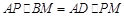
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,CD为△ABC外接圆的切线,AB的延长线交直线CD于点D, E,F分别为弦AB与弦AC上的点,且BC·AE=DC·AF,B, E, F,C四点共圆。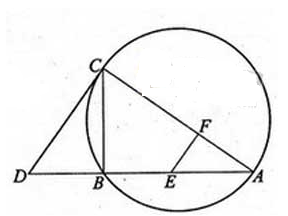
证明:(Ⅰ)CA是△ABC外接圆的直径;
(Ⅱ)若DB=BE=EA.求过B, E, F,C四点的圆的面积与△ABC外接圆面积的比值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题10分)已知C点在⊙O直径BE的延长线上,CA切⊙O于A 点,CD是∠ACB的平分线且交AE于点F,交AB于点D.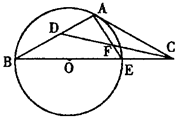
(1)求∠ADF的度数;
(2)若AB=AC,求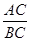 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图所示,四边形ABCD为矩形,点M是BC的中点,CN=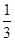 CA,用向量法证明:
CA,用向量法证明:
(1)D、N、M三点共线;(2)若四边形ABCD为正方形,则DN=BN. K^S*5U.C ^S*5U.C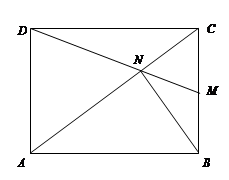

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com