
| A. | 12 | B. | 14 | C. | 6 | D. | 7 |
分析 根据函数f(x)是奇函数,且满足f(2-x)=f(x),推出函数的周期性,然后判断方程f(x)=-1在一个周期内实根的个数并求和,进而求出方程f(x)=1在区间[-1,7]上所有实根之和.
解答 解:由f(2-x)=f(x)知函数f(x)的图象关于直线x=1对称,
由f(x)是R上的奇函数知f(2-x)=-f(x-2),f(x-4)=-f(4-x)
在f(2-x)=f(x)中,以x-2代x得:
f(2-(x-2))=f(x-2)即f(4-x)=f(x-2),
所以f(x)=f(2-x)=-f(4-x)=f(x-4)
即f(x+4)=f(x),
所以f(x)是以4为周期的周期函数.
考虑f(x)的一个周期,例如[-1,3],
由f(x)在[0,1)上是减函数知f(x)在(1,2]上是增函数,
f(x)在(-1,0]上是减函数,f(x)在[2,3)上是增函数.
对于奇函数f(x)有f(0)=0,f(2)=f(2-2)=f(0)=0,
故当x∈(0,1)时,f(x)<f(0)=0,当x∈(1,2)时,f(x)<f(2)=0,
当x∈(-1,0)时,f(x)>f(0)=0,当x∈(2,3)时,f(x)>f(2)=0,
方程f(x)=-1在[0,1)上有实数根,
则这实数根是唯一的,因为f(x)在(0,1)上是单调函数,
则由于f(2-x)=f(x),故方程f(x)=-1在(1,2)上有唯一实数.
在(-1,0)和(2,3)上f(x)>0,
则方程f(x)=-1在(-1,0)和(2,3)上没有实数根.
从而方程f(x)=-1在一个周期内有且仅有两个实数根.
当x∈[-1,3],方程f(x)=-1的两实数根之和为x+2-x=2,
当x∈[-1,7],方程f(x)=-1的所有四个实数根之和为x+2-x+4+x+4+2-x=2+8+2=12.
故选:A.
点评 本题考查了函数的奇偶性、对称性、周期性、单调性等函数的重要性质,还考查了方程根的问题,综合性较强,解题的关键是根据奇偶性和对称性得出周期性.


科目:高中数学 来源: 题型:选择题

| A. | $\frac{8}{13}$ | B. | $\frac{17}{28}$ | C. | $\frac{2}{3}$ | D. | $\frac{18}{29}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 671 | B. | 672 | C. | 1342 | D. | 1344 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
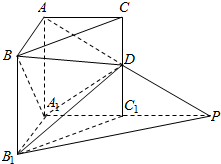 如图所示,在直三棱柱ABC-A1B1B1中,∠BAC=90°,AB=AC=AA1=1,P是AD的延长线与A1C1的延长线的交点,且PB1∥平面BDA1.
如图所示,在直三棱柱ABC-A1B1B1中,∠BAC=90°,AB=AC=AA1=1,P是AD的延长线与A1C1的延长线的交点,且PB1∥平面BDA1.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
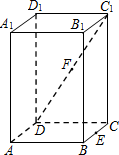 如图,在正四棱柱(底面是正方形的直棱柱)ABCD-A1B1C1D1中,E是BC的中点,F是C1D的中点,P是棱CC1所在直线上的动点.则下列四个命题:
如图,在正四棱柱(底面是正方形的直棱柱)ABCD-A1B1C1D1中,E是BC的中点,F是C1D的中点,P是棱CC1所在直线上的动点.则下列四个命题:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|X≥2} | B. | {x|x>2} | C. | {x|x≤0或x≥2} | D. | {x|0<x<2} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com