
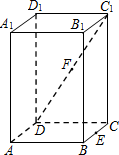
 如图,在正四棱柱(底面是正方形的直棱柱)ABCD-A1B1C1D1中,E是BC的中点,F是C1D的中点,P是棱CC1所在直线上的动点.则下列四个命题:
如图,在正四棱柱(底面是正方形的直棱柱)ABCD-A1B1C1D1中,E是BC的中点,F是C1D的中点,P是棱CC1所在直线上的动点.则下列四个命题:分析 根据标榜的结构特征,结合线面垂直的判定与性质,面面平行的判定与性质,锥体的体积公式,直线与平面的夹角等知识点,分别判断4个结论的真假,可得答案.
解答 解:由CD⊥平面BCC1B1,PE?平面BCC1B1,故①CD⊥PE正确;
连接ED1,则EF∥BD1,故EF∥平面ABC1D1,故②EF∥平面ABC1正确;
③${V}_{P-{A}_{1}D{D}_{1}}$=$\frac{1}{6}$${V}_{ABCD-{A}_{1}{B}_{1}{C}_{1}{D}_{1}}$,${V}_{{D}_{1}-ADE}$=$\frac{1}{6}$${V}_{ABCD-{A}_{1}{B}_{1}{C}_{1}{D}_{1}}$,故③${V_{P-{A_1}D{D_1}}}={V_{{D_1}-ADE}}$正确;
过P做一条与以ABCD为底面的正方体的对角线平行的直线,则该直线与正四棱柱的各个面都成等角.故④正确;
故正确命题的序号为:①③④,
故答案为:①②③④.
点评 本题考查的知识点是线面垂直的判定与性质,面面平行的判定与性质,锥体的体积公式,直线与平面的夹角,是立体几何知识的综合考查,难度中档.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | a<c<b | C. | b<c<a | D. | b<a<c |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | 14 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知直三棱柱ABC-A1B1C1中,AA1=AB=AC,AB⊥AC,M,N,Q分别是CC1,BC,AC的中点,点P在线段A1B1上运动.
如图,已知直三棱柱ABC-A1B1C1中,AA1=AB=AC,AB⊥AC,M,N,Q分别是CC1,BC,AC的中点,点P在线段A1B1上运动.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
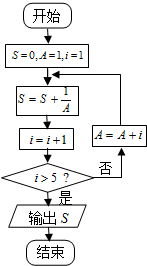
| A. | $\frac{3}{2}$ | B. | $\frac{5}{3}$ | C. | $\frac{8}{5}$ | D. | $\frac{12}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 540 | B. | 480 | C. | 360 | D. | 200 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com