
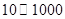 万元的投资收益.现公司准备制定一个对科研课题组的奖励方案:奖金
万元的投资收益.现公司准备制定一个对科研课题组的奖励方案:奖金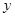 (单位:万元)随投资收益
(单位:万元)随投资收益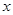 (单位:万元)的增加而增加,且奖金不低于
(单位:万元)的增加而增加,且奖金不低于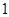 万元,同时不超过投资收益的
万元,同时不超过投资收益的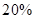 .
.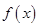 ,试用数学语言表述公司对奖励方案的函数模型
,试用数学语言表述公司对奖励方案的函数模型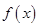 的基本要求.
的基本要求.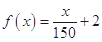 ; ②
; ②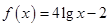
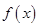 的基本要求转化为数学语言;(2)对题中的两个函数是否满足(1)中的三个限制条件进行验证,对于函数上述两个函数是否满足题中的条件,主要是研究函数的单调性与最值以及恒成立问题,可以利用基本函数的单调性以及利用导数来进行求解.
的基本要求转化为数学语言;(2)对题中的两个函数是否满足(1)中的三个限制条件进行验证,对于函数上述两个函数是否满足题中的条件,主要是研究函数的单调性与最值以及恒成立问题,可以利用基本函数的单调性以及利用导数来进行求解.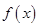 的基本要求是:
的基本要求是: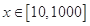 时,
时,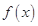 是增函数;②
是增函数;②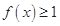 恒成立;③
恒成立;③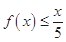 恒成立;
恒成立;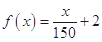 :当
:当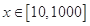 时,
时,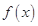 是增函数,
是增函数,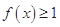 显然恒成立;
显然恒成立;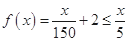 在
在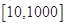 上恒成立,整理即
上恒成立,整理即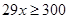 恒成立,而
恒成立,而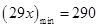 ,
,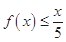 不恒成立.故该函数模型不符合公司要求.
不恒成立.故该函数模型不符合公司要求.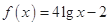 :
: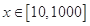 时,
时,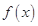 是增函数,则
是增函数,则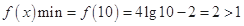 .∴
.∴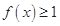 恒成立.
恒成立.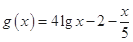 ,则
,则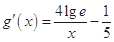 .
.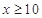 时,
时,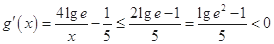 ,
,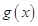 在
在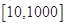 上是减函数,
上是减函数,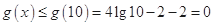 .
.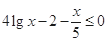 ,即
,即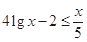 ,∴
,∴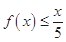 恒成立.
恒成立.

科目:高中数学 来源:不详 题型:填空题
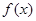 满足下列条件:对任意
满足下列条件:对任意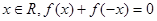 ,且对任意
,且对任意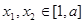
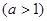 ,当
,当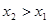 时,有
时,有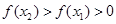 .给出下列四个结论:
.给出下列四个结论: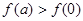 ②
②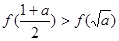
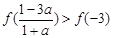 ④
④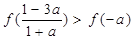
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
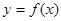 是R上的偶函数,对于
是R上的偶函数,对于 都有
都有 成立,且
成立,且 ,当
,当 ,且
,且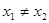 时,都有
时,都有 .则给出下列命题:
.则给出下列命题: ; ②函数
; ②函数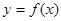 图象的一条对称轴为
图象的一条对称轴为 ;
;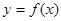 在[﹣9,﹣6]上为减函数; ④方程
在[﹣9,﹣6]上为减函数; ④方程 在[﹣9,9]上有4个根;
在[﹣9,9]上有4个根;| A.1 | B.2 | C.3 | D.4 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
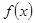 的定义域内任意两个自变量的值
的定义域内任意两个自变量的值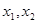 ,当
,当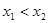 时,都有
时,都有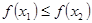 且存在两个不相等的自变量
且存在两个不相等的自变量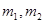 ,使得
,使得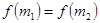 ,则称
,则称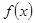 为定义域上的不严格的增函数.已知函数
为定义域上的不严格的增函数.已知函数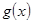 的定义域、值域分别为
的定义域、值域分别为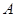 ,
,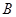 ,
,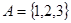 ,
,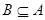 且
且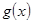 为定义域
为定义域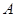 上的不严格的增函数,那么这样的函数
上的不严格的增函数,那么这样的函数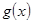 共有________个.
共有________个. 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com