
| A. | ①② | B. | ③④ | C. | ②③ | D. | ①④ |
分析 利用正弦函数的图象和性质,逐一判断各个各个选项是否正确,从而得出结论.
解答 解:对于函数$f(x)=4sin(2x+\frac{π}{3})(x∈R)$,由于f(x)=4cos[$\frac{π}{2}$-(2x+$\frac{π}{3}$)]=4cos(2x-$\frac{π}{6}$),故①正确;
当x=-$\frac{π}{6}$时,f(x)=0,故y=f(x)的图象关于点$(-\frac{π}{6},0)$对称,故②正确;
由于f(x)的周期为$\frac{2π}{2}$=π,故③错误;
当x=$\frac{5π}{6}$时,f(x)=0,故y=f(x)的图象不关于直线$x=\frac{5π}{6}$对称,故排除④,
故选:A.
点评 本题主要考查正弦函数的图象和性质,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\sqrt{3}$ | C. | 3 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
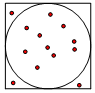 某同学动手做实验:《用随机模拟的方法估计圆周率的值》,在如图的正方形中随机撒豆子,每个豆子落在正方形内任何一点是等可能的,若他随机地撒500粒统计得到落在圆内的豆子数为390粒,则由此估计出的圆周率π的值为3.12.(精确到0.01)
某同学动手做实验:《用随机模拟的方法估计圆周率的值》,在如图的正方形中随机撒豆子,每个豆子落在正方形内任何一点是等可能的,若他随机地撒500粒统计得到落在圆内的豆子数为390粒,则由此估计出的圆周率π的值为3.12.(精确到0.01)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ${d_n}=\frac{{{c_1}+{c_2}+…+{c_n}}}{n}$ | B. | ${d_n}=\frac{{{c_1}•{c_2}{•_{\;}}{…_{\;}}•{c_n}}}{n}$ | ||
| C. | ${d_n}=\root{n}{{{c_1}•{c_2}{•_{\;}}{…_{\;}}•{c_n}}}$ | D. | ${d_n}=\root{n}{{\frac{{{c_1}^n•{c_2}^n{•_{\;}}{…_{\;}}•{c_n}^n}}{n}}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com