
分析 (Ⅰ)由等差数列通项公式和等比数列性质求出d=a,由此能求出数列{an}的通项公式及Sn.
(Ⅱ)由$\frac{1}{{S}_{n}}=\frac{2}{a}(\frac{1}{n}-\frac{1}{n+1})$,利用裂项求和法能求出Bn,由cn=$\frac{1}{{a}_{{2}^{n-1}}}$=$\frac{1}{a•{2}^{n-1}}$,能求出Cn,由此能比较Bn与Cn的大小.
解答 解:(Ⅰ)设等差数列的公差为d,
∵公差不为0的等差数列{an}的首项a1=a(a>0),该数列的前n项和为Sn,且$\frac{1}{{a}_{1}}$,$\frac{1}{{a}_{2}}$,$\frac{1}{{a}_{4}}$成等比数列,
∴($\frac{1}{{a}_{2}}$)2=$\frac{1}{{a}_{1}}•\frac{1}{{a}_{4}}$,∴$({a}_{1}+d)^{2}={a}_{1}({a}_{1}+3d)$,
解得d=a或d=0(舍),
∴an=a+(n-1)a=na.
Sn=$na+\frac{n(n-1)}{2}a$=$\frac{an(n+1)}{2}$.
(Ⅱ)∵bn=$\frac{1}{{S}_{n}}$,cn=$\frac{1}{{a}_{{2}^{n-1}}}$,且Bn,Cn分别为数列{bn},{cn}的前n项和,
$\frac{1}{{S}_{n}}=\frac{2}{a}(\frac{1}{n}-\frac{1}{n+1})$,
∴Bn=$\frac{2}{a}(1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+…+\frac{1}{n}-\frac{1}{n+1})$=$\frac{2}{a}(1-\frac{1}{n+1})$,
∵cn=$\frac{1}{{a}_{{2}^{n-1}}}$=$\frac{1}{a•{2}^{n-1}}$,
∴Cn=$\frac{1}{{a}_{1}}+\frac{1}{{a}_{2}}+\frac{1}{{a}_{{2}^{2}}}$+…+$\frac{1}{{a}_{{2}^{n-1}}}$=$\frac{1}{a}•\frac{1-(\frac{1}{2})^{n}}{1-\frac{1}{2}}$=$\frac{2}{a}(1-\frac{1}{{2}^{n}})$,
当n≥2时,${2}^{n}={C}_{n}^{0}+{C}_{n}^{1}+{C}_{n}^{2}+…+{C}_{n}^{n}$>n+1,
∴1-$\frac{1}{n+1}$<1-$\frac{1}{{2}^{n}}$,
∴当a>0时,Bn<Cn.
点评 本题考查等差数列、等比数列、求和公式、不等式等基础知识,同时考查分类讨论思想、考查分析问题、解决问题的能力.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源: 题型:解答题
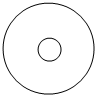 某家庭游戏中有这样一个“投币”活动,活动道具是如图所示的半径为10cm的圆形纸板,纸板上有一个相同圆心、半径为2cm的小圆,现让家庭中的每名成员向此纸板抛掷一枚半径为1cm的硬币,使硬币整体随机落在纸板内,若硬币落下后与小圆圆面(不包含边界)无公共点则中奖,否则不中奖.
某家庭游戏中有这样一个“投币”活动,活动道具是如图所示的半径为10cm的圆形纸板,纸板上有一个相同圆心、半径为2cm的小圆,现让家庭中的每名成员向此纸板抛掷一枚半径为1cm的硬币,使硬币整体随机落在纸板内,若硬币落下后与小圆圆面(不包含边界)无公共点则中奖,否则不中奖.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{7π}{12}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1或i | C. | i | D. | -i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{1}{4}$,$\frac{1}{3}$] | B. | [$\frac{1}{4}$,$\frac{1}{3}$) | C. | [$\frac{1}{5}$,$\frac{1}{3}$) | D. | [$\frac{1}{5}$,$\frac{1}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
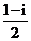 .
.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com