
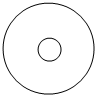
 某家庭游戏中有这样一个“投币”活动,活动道具是如图所示的半径为10cm的圆形纸板,纸板上有一个相同圆心、半径为2cm的小圆,现让家庭中的每名成员向此纸板抛掷一枚半径为1cm的硬币,使硬币整体随机落在纸板内,若硬币落下后与小圆圆面(不包含边界)无公共点则中奖,否则不中奖.
某家庭游戏中有这样一个“投币”活动,活动道具是如图所示的半径为10cm的圆形纸板,纸板上有一个相同圆心、半径为2cm的小圆,现让家庭中的每名成员向此纸板抛掷一枚半径为1cm的硬币,使硬币整体随机落在纸板内,若硬币落下后与小圆圆面(不包含边界)无公共点则中奖,否则不中奖.分析 (1)由题意可得,硬币要落在纸板内,硬币圆心距离纸板圆心的距离应该小于9.硬币与小圆无公共点,硬币圆心距离小圆圆心要大于2,先求出硬币落在纸板上的面积,然后再求解硬币落下后与小圆没交点的区域的面积,代入古典概率的计算公式可求中奖的概率.
(2)由题意E~B(3,$\frac{8}{9}$),由此能求出E的分布列和数学期望.
解答 解:(1)记“中奖”为事件A
硬币要落在纸板内,硬币圆心距离纸板圆心的距离应该小于9,其面积为81π
无公共点也就意味着,硬币的圆心与纸板的圆心相距超过3cm
以纸板的圆心为圆心,作一个半径3cm的圆,硬币的圆心在此圆外面,则硬币与半径为2cm的小圆无公共点,此半径为3的圆面积是9π
所以有公共点的概率为$\frac{9π}{81π}$=$\frac{1}{9}$,
中奖的概率P(A)=1-$\frac{1}{9}$=$\frac{8}{9}$.
(2)由题意E~B(3,$\frac{8}{9}$),
P(E=0)=${C}_{3}^{0}(\frac{1}{9})^{3}$=$\frac{1}{729}$,
P(E=1)=${C}_{3}^{1}(\frac{8}{9})(\frac{1}{9})^{2}$=$\frac{24}{729}$,
P(E=2)=${C}_{3}^{2}(\frac{8}{9})^{2}(\frac{1}{9})$=$\frac{192}{729}$,
P(E=3)=${C}_{3}^{3}(\frac{8}{9})^{3}$=$\frac{512}{729}$,
∴E的分布列为:
| E | 0 | 1 | 2 | 3 |
| P | $\frac{1}{729}$ | $\frac{24}{729}$ | $\frac{192}{729}$ | $\frac{512}{729}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意二项分布的性质的合理运用.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充要 | D. | 既不充分又不必要 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$i | B. | -$\frac{1}{2}$-$\frac{\sqrt{3}}{2}$i | C. | $\frac{1}{2}$+$\frac{\sqrt{3}}{2}$i | D. | $\frac{1}{2}$-$\frac{\sqrt{3}}{2}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | -$\sqrt{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | -$\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com