
分析 (1)由向量垂直得到${S}_{n}=\frac{1}{4}{n}^{2}+\frac{3}{4}n$,由此能求出an.
(2)由$\frac{1}{(2{a}_{n}+1)n}$=$\frac{1}{n(n+2)}$=$\frac{1}{2}$($\frac{1}{n}-\frac{1}{n+2}$),利用裂项求和法能证明Tn<$\frac{3}{4}$.
解答 解:(1)∵Sn为数列{an}的前n项和,且向量$\overrightarrow{a}$=(-4,n),$\overrightarrow{b}$=(Sn,n+3)垂直,
∴$\overrightarrow{a}•\overrightarrow{b}$=-4Sn+n(n+3)=0,∴${S}_{n}=\frac{1}{4}{n}^{2}+\frac{3}{4}n$,
∴n=1时,${S}_{1}={a}_{1}=\frac{1}{4}+\frac{3}{4}$=1,
n≥2时,an=Sn-Sn-1=($\frac{1}{4}{n}^{2}+\frac{3}{4}n$)-[$\frac{1}{4}(n-1)^{2}+\frac{3}{4}(n-1)$]=$\frac{n}{2}+\frac{1}{2}$.
n=1时,上式成立,
∴an=$\frac{n}{2}+\frac{1}{2}$.
证明:(2)∵$\frac{1}{(2{a}_{n}+1)n}$=$\frac{1}{n(n+2)}$=$\frac{1}{2}$($\frac{1}{n}-\frac{1}{n+2}$),
∴数列{$\frac{1}{(2{a}_{n}+1)n}$}前n项和:
Tn=$\frac{1}{2}$(1-$\frac{1}{3}+\frac{1}{2}-\frac{1}{4}+\frac{1}{3}-\frac{1}{5}$+…+$\frac{1}{n-1}-\frac{1}{n+1}+\frac{1}{n}-\frac{1}{n+2}$)
=$\frac{1}{2}$(1+$\frac{1}{2}$-$\frac{1}{n+1}-\frac{1}{n+2}$)
=$\frac{3}{4}$-$\frac{1}{n+1}-\frac{1}{n+2}$,
∴Tn<$\frac{3}{4}$.
点评 本题考查数列的通项公式的求法,考查不等式的证明,是中档题,解题时要认真审题,注意裂项求和法的合理运用.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:高中数学 来源: 题型:选择题
| A. | 2015 | B. | 2016 | C. | 4030 | D. | 4032 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
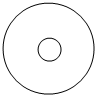 某家庭游戏中有这样一个“投币”活动,活动道具是如图所示的半径为10cm的圆形纸板,纸板上有一个相同圆心、半径为2cm的小圆,现让家庭中的每名成员向此纸板抛掷一枚半径为1cm的硬币,使硬币整体随机落在纸板内,若硬币落下后与小圆圆面(不包含边界)无公共点则中奖,否则不中奖.
某家庭游戏中有这样一个“投币”活动,活动道具是如图所示的半径为10cm的圆形纸板,纸板上有一个相同圆心、半径为2cm的小圆,现让家庭中的每名成员向此纸板抛掷一枚半径为1cm的硬币,使硬币整体随机落在纸板内,若硬币落下后与小圆圆面(不包含边界)无公共点则中奖,否则不中奖.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
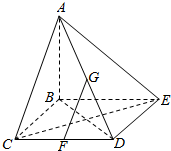 在四棱锥A-BCDE中,AB⊥平面BCDE,底面BCDE是正方形且AB=CD,点G,F分别是AD和CD的中点.求:
在四棱锥A-BCDE中,AB⊥平面BCDE,底面BCDE是正方形且AB=CD,点G,F分别是AD和CD的中点.求:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1或i | C. | i | D. | -i |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com