
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充要 | D. | 既不充分又不必要 |
分析 先看当c=b时,判断出三角形为等腰三角形,可推断出C=B,进而可求得ccosC=bcosB,推断出充分性;再看若ccosC=bcosB,利用正弦定理把边转化成角的正弦,利用二倍角公式求得C=B或C+B=$\frac{π}{2}$,推断出条件是不必要的,最后综合可得答案.
解答 解:若c=b,则C=B,∴ccosC=bcosB,条件是充分的;
若ccosC=bcosB
∴sinCcosC=sinBcosB,∴sin2C=sin2B,
∴2C=2B或2C+2B=π,即C=B或C+B=$\frac{π}{2}$,
故条件是不必要的.
故选:A.
点评 本题主要考查了充分条件,必要条件和充分必要条件的判定,正弦定理的应用.充分必要关系是两个命题之间的逻辑关系,是解题中实现命题变更(转化)的依据.两个命题之间有充分不必要,必要不充分、充分且必要、既不充分又不必要四类关系.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | y=sin(2x-$\frac{π}{2}$) | B. | y=cos(2x-$\frac{π}{2}$) | C. | y=10x+10-x | D. | y=ln(x2+1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2015 | B. | 2016 | C. | 4030 | D. | 4032 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
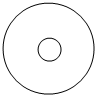 某家庭游戏中有这样一个“投币”活动,活动道具是如图所示的半径为10cm的圆形纸板,纸板上有一个相同圆心、半径为2cm的小圆,现让家庭中的每名成员向此纸板抛掷一枚半径为1cm的硬币,使硬币整体随机落在纸板内,若硬币落下后与小圆圆面(不包含边界)无公共点则中奖,否则不中奖.
某家庭游戏中有这样一个“投币”活动,活动道具是如图所示的半径为10cm的圆形纸板,纸板上有一个相同圆心、半径为2cm的小圆,现让家庭中的每名成员向此纸板抛掷一枚半径为1cm的硬币,使硬币整体随机落在纸板内,若硬币落下后与小圆圆面(不包含边界)无公共点则中奖,否则不中奖.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com