
【题目】如图,三棱锥![]() 的底面是边长为3的等边三角形,侧棱
的底面是边长为3的等边三角形,侧棱![]() 设点M,N分别为PC,BC的中点.
设点M,N分别为PC,BC的中点.
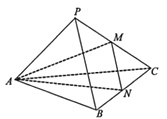
(Ⅰ)求证:BC⊥面AMN;
(Ⅱ)求直线AP与平面AMN所成角.
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案科目:高中数学 来源: 题型:
【题目】向体积为1的正方体密闭容器内注入体积为![]() 的液体,旋转容器,下列说法正确的是( )
的液体,旋转容器,下列说法正确的是( )
A.当![]() 时,容器被液面分割而成的两个几何体完全相同
时,容器被液面分割而成的两个几何体完全相同
B.![]() ,液面都可以成正三角形形状
,液面都可以成正三角形形状
C.当液面与正方体的某条体对角线垂直时,液面面积的最大值为![]()
D.当液面恰好经过正方体的某条体对角线时,液面边界周长的最小值为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于圆周率π,数学发展史上出现过许多很有创意的求法,如著名的蒲丰实验和查理斯实验,受其启发,我们也可以通过设计下面的实验来估计π的值,先请240名同学,每人随机写下两个都小于1的正实数x,y组成的实数对(x,y);若将(x,y)看作一个点,再统计点(x,y)在圆x2+y2=1外的个数m;最后再根据统计数m来估计π的值,假如统计结果是m=52,那么可以估计π的近似值为_______.(用分数表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电讯企业为了了解某地区居民对电讯服务质量评价情况,随机调查100 名用户,根据这100名用户对该电讯企业的评分,绘制频率分布直方图,如图所示,其中样本数据分组为![]() ,
,![]() ,……
,……![]() .
.
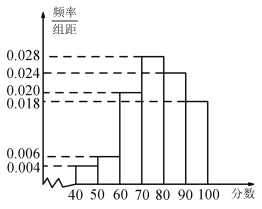
(1)估计该地区用户对该电讯企业评分不低于70分的概率,并估计对该电讯企业评分的中位数;
(2)现从评分在![]() 的调查用户中随机抽取2人,求2人评分都在
的调查用户中随机抽取2人,求2人评分都在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是某市3月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择3月1日至3月13日中的某一天到达该市,并停留2天.
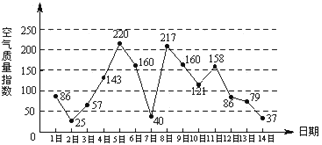
(Ⅰ)求此人到达当日空气重度污染的概率;
(Ⅱ)设X是此人停留期间空气质量优良的天数,求X的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】流行病学资料显示,![]() 岁以上男性静息心率过高将会增加患心血管疾病的风险,相反,静息心率相对稳定的
岁以上男性静息心率过高将会增加患心血管疾病的风险,相反,静息心率相对稳定的![]() 到
到![]() 岁的男性,在未来
岁的男性,在未来![]() 年内患心血管疾病的几率会降低
年内患心血管疾病的几率会降低![]() .研究员们还表示,其中静息心率超过
.研究员们还表示,其中静息心率超过![]() (次/分)的人比静息心率低于
(次/分)的人比静息心率低于![]() 的人罹患心血管疾病的风险高出一倍.某单位对其所有的离、退休老人进行了静息心率监测,其中一次静息心率的茎叶图和频率分布直方图如下,其中,频率分布直方图的分组区间分别为
的人罹患心血管疾病的风险高出一倍.某单位对其所有的离、退休老人进行了静息心率监测,其中一次静息心率的茎叶图和频率分布直方图如下,其中,频率分布直方图的分组区间分别为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,由于扫描失误,导致部分数据丢失.据此解答如下问题:
,由于扫描失误,导致部分数据丢失.据此解答如下问题:
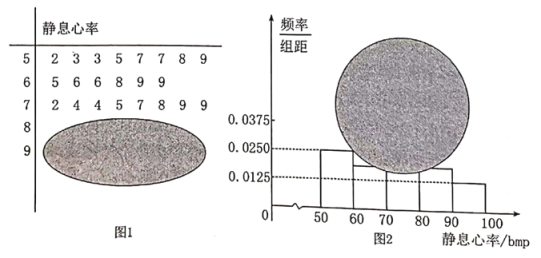
(1)求此单位离、退休人员总数和静息心率在![]() 之间的频率;
之间的频率;
(2)现从静息心率在![]() 之间的数据中任取
之间的数据中任取![]() 份分析离、退休人员身体情况,设抽取的静息心率在
份分析离、退休人员身体情况,设抽取的静息心率在![]() 的份数为
的份数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 在椭圆
在椭圆![]() :
: ![]() 上,
上, ![]() 是椭圆的一个焦点.
是椭圆的一个焦点.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)椭圆C上不与![]() 点重合的两点
点重合的两点![]() ,
, ![]() 关于原点O对称,直线
关于原点O对称,直线![]() ,
, ![]() 分别交
分别交![]() 轴于
轴于![]() ,
, ![]() 两点.求证:以
两点.求证:以![]() 为直径的圆被直线
为直径的圆被直线![]() 截得的弦长是定值.
截得的弦长是定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com