
分析 根据角240°的终边与单位圆的交点的横坐标是cos240°、角240°的终边与单位圆的交点的纵坐标是sin240°,即可求出角240°的终边与单位圆的交点的坐标.
解答 解:由于角240°的终边与单位圆的交点的横坐标是cos240°=-$\frac{1}{2}$,
由于角240°的终边与单位圆的交点的纵坐标是sin240°=-$\frac{\sqrt{3}}{2}$,
∴角240°的终边与单位圆的交点的坐标是(-$\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$),
故答案为(-$\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$).
点评 本题主要考查任意角的三角函数的定义,属于基础题.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案科目:高中数学 来源: 题型:解答题
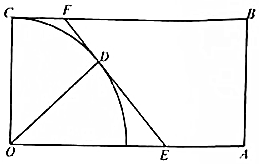 如图,矩形公园OABC中,OA=2km,OC=1km,公园的左下角阴影部分为以O为圆心,半径为1km的$\frac{1}{4}$圆面的人工湖,现计划修建一条与圆相切的观光道路EF(点E、F分别在边OA与BC上),D为切点.
如图,矩形公园OABC中,OA=2km,OC=1km,公园的左下角阴影部分为以O为圆心,半径为1km的$\frac{1}{4}$圆面的人工湖,现计划修建一条与圆相切的观光道路EF(点E、F分别在边OA与BC上),D为切点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\frac{2}{{3{e^2}}},\frac{1}{e})$ | B. | $[\frac{2}{{3{e^2}}},\frac{1}{e})$ | C. | $(\frac{2}{{3{e^2}}},\frac{1}{2e})$ | D. | $[\frac{2}{{3{e^2}}},\frac{1}{2e})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com