
分析 (1)设与$\frac{x^2}{9}-\frac{y^2}{4}=1$共渐近线的双曲线的方程为$\frac{x^2}{9}-\frac{y^2}{4}=λ$,将点(3,4)代入双曲线中,求出λ=-3,
即可得到双曲线的方程.
(2)设A(x1,y1),B(x2,y2),P(x0,y0),将A,B坐标代入椭圆,利用平方差法,由直线AB的斜率为-1可得,求出OP的斜率为$\frac{y_0}{x_0}=\frac{1}{2}$,推出a2=2b2,通过$c=\sqrt{3}$,求解即可.
解答 解:(1)设与$\frac{x^2}{9}-\frac{y^2}{4}=1$共渐近线的双曲线的方程为$\frac{x^2}{9}-\frac{y^2}{4}=λ$,
将点(3,4)代入双曲线中,可得$\frac{9}{9}-\frac{16}{4}=λ$,即λ=-3,
代入$\frac{x^2}{9}-\frac{y^2}{4}=λ$可得,双曲线的方程为$\frac{y^2}{12}-\frac{x^2}{27}=1$.
(2)设A(x1,y1),B(x2,y2),P(x0,y0),
将A,B坐标代入椭圆可得,$\left\{{\begin{array}{l}{\frac{x_1^2}{a^2}+\frac{y_1^2}{b^2}=1(1)}\\{\frac{x_2^2}{a^2}+\frac{y_2^2}{b^2}=1(2)}\end{array}}\right.$,
(1)-(2)可得,$\frac{{{y_2}-{y_1}}}{{{x_2}-{x_1}}}=-\frac{b^2}{a^2}•\frac{x_0}{y_0}$,
由直线AB的斜率为-1可得,$-\frac{b^2}{a^2}•\frac{x_0}{y_0}=-1$,而OP的斜率为$\frac{y_0}{x_0}=\frac{1}{2}$,
所以a2=2b2,
直线$x+y-\sqrt{3}=0$过椭圆的右焦点,可得$c=\sqrt{3}$,
由a2=b2+c2,得到a2=6,b2=3,
所以椭圆的标准方程为$\frac{x^2}{6}+\frac{y^2}{3}=1$.
点评 本题考查直线与双曲线的位置关系,直线与椭圆的位置关系的应用,双曲线方程以及椭圆方程的求法,考查转化思想以及计算能力.


科目:高中数学 来源: 题型:选择题
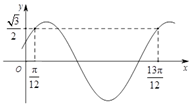 已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则( )
已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则( )| A. | ω=2,$φ=\frac{π}{6}$ | B. | $ω=\frac{1}{2}$,$φ=\frac{π}{6}$ | C. | ω=2,$φ=\frac{π}{3}$ | D. | $ω=\frac{1}{2}$,$φ=\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知抛物线E:y2=2px(p>0)的焦点过为F,过F且倾斜角为$\frac{π}{4}$的直线l被E截得的线段长为8.
已知抛物线E:y2=2px(p>0)的焦点过为F,过F且倾斜角为$\frac{π}{4}$的直线l被E截得的线段长为8.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 120° | B. | 30° | C. | 90° | D. | 60° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{5}{2}i$ | B. | $-\frac{5}{2}$ | C. | $-\frac{1}{2}i$ | D. | $-\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com