
分析 利用定义法结合分式函数的性质进行求解即可.
解答 解:任取x1,x2∈(-2,+∞),且x1<x2,…(2分)
则f(x1)-f(x2)=$\frac{1-2a}{{x}_{1}+2}$-$\frac{1-2a}{{x}_{2}+2}$=$\frac{(1-2a)({x}_{2}-{x}_{1})}{({x}_{1}+2)({x}_{2}+2)}$.…(5分)
∵函数f(x)=$\frac{1-2a}{x+2}$在区间(-2,+∞)上为增函数,
∴f(x1)-f(x2)<0.…(7分)
∵x2-x1>0,x1+2>0,x2+2>0,
∴1-2a<0,故a>$\frac{1}{2}$.…(10分)
即实数a的取值范围是($\frac{1}{2}$,+∞).…(12分)
点评 本题主要考查函数单调性的应用,利用分式函数的性质以及函数单调性的定义是解决本题的关键.


 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:高中数学 来源: 题型:解答题
| 年份 | 2009 | 2010 | 2011 | 2012 | 2013 |
| 年份代号x | 1 | 2 | 3 | 4 | 5 |
| 人均纯收入y | 2.8 | 3.2 | 4.2 | 4.8 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
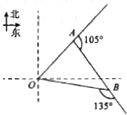 如图,一只蜘蛛从点O出发沿北偏东45°方向爬行xcm,到达点A处捕捉到一只小虫,然后沿OA方向右转105°爬行10cm,到达点B处捕捉哦另一只小虫,这时他沿AB方向右转135°爬行回到它的出发点O处,那么x=$\frac{10\sqrt{6}}{3}$.
如图,一只蜘蛛从点O出发沿北偏东45°方向爬行xcm,到达点A处捕捉到一只小虫,然后沿OA方向右转105°爬行10cm,到达点B处捕捉哦另一只小虫,这时他沿AB方向右转135°爬行回到它的出发点O处,那么x=$\frac{10\sqrt{6}}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | -4 | C. | $-\frac{1}{4}$ | D. | $-\frac{9}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com