Question

18．图（1）、（2）、（3）、（4）分别包含1个、5个、13个、25个第二十九届北京奥运会吉祥物“福娃迎迎”，按同样的方式构造图形，设第n个图形包含f（n）个“福娃迎迎”．

（1）求出f（5）；
（2）利用合情推理的“归纳推理思想”归纳出f（n+1）与f（n）的关系式（不需写出证明过程）；
（3）根据你得到的关系式求f（n）的表达式．

Answer 1

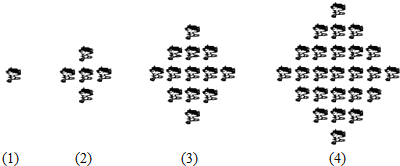
分析 （1）由题意，可以求出f（5）；
（2）考查相邻两项的关系可得出f（n+1）-f（n）=4n；
（3）由累加法可求得f（n）=2n²-2n+1，由此可求出答案．

解答 解：（1）∵f（1）=1，f（2）=5，f（3）=13，f（4）=25，
∴f（5）=25+4×4=41．…（4分）
（2）∵f（2）-f（1）=4=4×1，f（3）-f（2）=8=4×2，
f（4）-f（3）=12=4×3，f（5）-f（4）=16=4×4，
由上式规律得出f（n+1）-f（n）=4n．…（10分）
（3）∵f（2）-f（1）=4×1，f（3）-f（2）=4×2，f（4）-f（3）=4×3，f（n-1）-f（n-2）=4•（n-2），f（n）-f（n-1）=4•（n-1），
∴f（n）-f（1）=4[1+2++（n-2）+（n-1）]=2（n-1）•n，…（14分）
∴f（n）=2n²-2n+1（n≥2），
∵f（1）=1也满足上式，∴f（n）=2n²-2n+1． …（16分）

点评 本题考查归纳推理，解题的关键是研究相邻两项的关系得出递推公式，再由累加法得出项的表达式，本题考查了分析归纳的能力，属于中档题．