Question

18．已知向量$\overrightarrow{a}$⊥$\overrightarrow{b}$，|$\overrightarrow{a}$-$\overrightarrow{b}$|=2，定义：c_λ=λ$\overrightarrow{a}$+（1-λ）$\overrightarrow{b}$，其中0≤λ≤1．若${c_λ}•{c_{\frac{1}{2}}}=\frac{1}{2}$，则|c_λ|的值不可能为（　　）

• A． $\frac{{\sqrt{5}}}{5}$
• B． $\frac{{\sqrt{3}}}{3}$
• C． $\frac{{\sqrt{2}}}{2}$
• D． 1

Answer 1

分析 由题意可得$|\overrightarrow{{c}_{\frac{1}{2}}}|=1$，设$\overrightarrow{AB}=\overrightarrow{a}，\overrightarrow{AC}=\overrightarrow{b}，\overrightarrow{AD}=\overrightarrow{{c}_{\frac{1}{2}}}，\overrightarrow{AP}=\overrightarrow{{c}_{λ}}$，则B，C，D，P四点共线，在圆中画出图形，由${c_λ}•{c_{\frac{1}{2}}}=\frac{1}{2}$得到两向量夹角的范围，从而求得|c_λ|的范围得答案．

解答 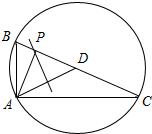解：∵向量$\overrightarrow{a}$⊥$\overrightarrow{b}$，|$\overrightarrow{a}$-$\overrightarrow{b}$|=2，∴以$\overrightarrow{a}，\overrightarrow{b}$为邻边的平行四边形为长方形，
则$|\overrightarrow{a}+\overrightarrow{b}|=|\overrightarrow{a}-\overrightarrow{b}|=2$，
又$\overrightarrow{{c}_{λ}}$=λ$\overrightarrow{a}$+（1-λ）$\overrightarrow{b}$，∴$\overrightarrow{{c}_{\frac{1}{2}}}=\frac{1}{2}\overrightarrow{a}+\frac{1}{2}\overrightarrow{b}=\frac{1}{2}（\overrightarrow{a}+\overrightarrow{b}）$，
则$|\overrightarrow{{c}_{\frac{1}{2}}}|=|\frac{1}{2}（\overrightarrow{a}+\overrightarrow{b}）|=\frac{1}{2}$$|\overrightarrow{a}+\overrightarrow{b}|$=1．
设$\overrightarrow{AB}=\overrightarrow{a}，\overrightarrow{AC}=\overrightarrow{b}，\overrightarrow{AD}=\overrightarrow{{c}_{\frac{1}{2}}}，\overrightarrow{AP}=\overrightarrow{{c}_{λ}}$，
由$\overrightarrow{{c}_{λ}}$=λ$\overrightarrow{a}$+（1-λ）$\overrightarrow{b}$，0≤λ≤1，可知B，C，D，P四点共线，
如右图，
设$＜\overrightarrow{{c}_{\frac{1}{2}}}，\overrightarrow{{c}_{λ}}＞=θ$，
∵${c_λ}•{c_{\frac{1}{2}}}=\frac{1}{2}$，∴由$\frac{1}{2}=\overrightarrow{{c}_{λ}}•\overrightarrow{{c}_{\frac{1}{2}}}$=$|\overrightarrow{{c}_{λ}}|cosθ$，得$\overrightarrow{{c}_{λ}}$在$\overrightarrow{{c}_{\frac{1}{2}}}$上的投影为$\frac{1}{2}$，
∴当B、P两点重合时，$|\overrightarrow{{c}_{λ}}|=|\overrightarrow{{c}_{\frac{1}{2}}}|$=1，$θ=\frac{π}{3}$，
当P、D重合时，θ=0．
∴$|\overrightarrow{{c}_{λ}}|=\frac{1}{2cosθ}$，θ∈（0，$\frac{π}{3}$]，cosθ∈[$\frac{1}{2}$，1），
∴$|\overrightarrow{{c}_{λ}}|∈（\frac{1}{2}，1]$．
则|c_λ|的值不可能为$\frac{\sqrt{5}}{5}$．
故选：A．

点评 本题考查平面向量的几何意义，涉及到向量的加、减法运算法则，三点共线的向量表示，向量的投影等知识，注意解题方法的积累，属于难题．