
| A. | 相交 | B. | 相离 | C. | 相切 | D. | 内含 |
分析 利用双曲线的定义,通过圆心距判断出当点P分别在左、右两支时,利用两圆圆心距离和半径之间的关系判断两圆相内切、外切.
解答 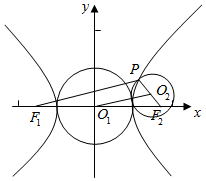
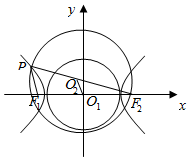 解:设以实轴|F1F2|为直径的圆的圆心为O1,其半径r1=a,
解:设以实轴|F1F2|为直径的圆的圆心为O1,其半径r1=a,
线段PF2为直径的圆的圆心为O2,其半径为r2=$\frac{|P{F}_{2}|}{2}$,
当P在双曲线左支上时,|O1O2|=$\frac{|P{F}_{1}|}{2}$,
∵r2-|O1O2|=$\frac{|P{F}_{2}|}{2}$-$\frac{|P{F}_{1}|}{2}$=a=r1,
∴两圆内切.
当P在双曲线右支上时,
|O1O2|=$\frac{|P{F}_{1}|}{2}$,
∵|O1O2|-r2=$\frac{|P{F}_{1}|}{2}$-$\frac{|P{F}_{2}|}{2}$=a=r1,
∴r1+r2=|O1O2|
∴两圆外切.
综上两圆相切,
故选:C.
点评 本题主要考查双曲线的性质的应用以及两圆位置关系的判断,利用双曲线的定义结合两圆位置关系的定义是解决本题的关键.注意要对P进行分类讨论.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:高中数学 来源: 题型:填空题
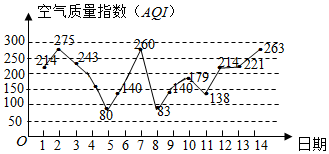 如图所示是某市2016年2月1日至14日的空气质量指数趋势图,空气质量指数(AQI)小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某同志随机选择2月1日至2月12日中的某一天到达该市,并停留3天.该同志到达当日空气质量优良的概率$\frac{1}{6}$.
如图所示是某市2016年2月1日至14日的空气质量指数趋势图,空气质量指数(AQI)小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某同志随机选择2月1日至2月12日中的某一天到达该市,并停留3天.该同志到达当日空气质量优良的概率$\frac{1}{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在区间[-$\frac{π}{12}$,$\frac{5}{12}$π]上单调递增 | B. | 在区间[$\frac{π}{4},\frac{π}{4}$]上单调递增 | ||
| C. | 在区间[$\frac{π}{4}$,$\frac{3π}{4}$]上单调递减 | D. | 在区间[-$\frac{π}{12}$,$\frac{5}{12}$π]上单调递减 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com