
【题目】四棱锥![]() ,底面
,底面![]() 为平行四边形,侧面
为平行四边形,侧面![]() 底面
底面![]() .已知
.已知![]() ,
,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 的中点.
的中点.
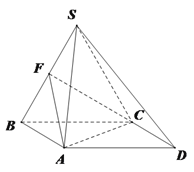
(1)求证:![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣ ![]() x2 , g(x)=
x2 , g(x)= ![]() x2+x,m∈R,令F(x)=f(x)+g(x). (Ⅰ)求函数f(x)的单调递增区间;
x2+x,m∈R,令F(x)=f(x)+g(x). (Ⅰ)求函数f(x)的单调递增区间;
(Ⅱ)若关于x的不等式F(x)≤mx﹣1恒成立,求整数m的最小值;
(Ⅲ)若m=﹣1,且正实数x1 , x2满足F(x1)=﹣F(x2),求证:x1+x2 ![]() ﹣1.
﹣1.
查看答案和解析>>
科目:高中数学 来源: 题型:
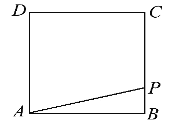
【题目】在边长为4的正方形ABCD的边上有一点P,沿着折线BCDA由点B(起点)向点A(终点)运动.设点P运动的路程为x,△APB的面积为y,且y与x之间的函数关系式用如图所示的程序框图给出.
(1)写出程序框图中①,②,③处应填充的式子.
(2)若输出的面积y值为6,则路程x的值为多少?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[2019·牡丹江一中]某校从参加高一年级期末考试的学生中抽取60名学生的成绩(均为整数),其成绩的频率分布直方图如图所示,由此估计此次考试成绩的中位数,众数和平均数分别是( )
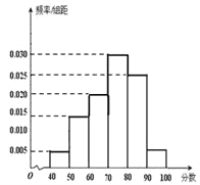
A. 73.3,75,72 B. 73.3,80,73
C. 70,70,76 D. 70,75,75
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】A市某机构为了调查该市市民对我国申办2034年足球世界杯的态度,随机选取了140位市民进行调查,调查结果统计如下:
支持 | 不支持 | 总计 | |
男性市民 | 60 | ||
女性市民 | 50 | ||
合计 | 70 | 140 |
(I)根据已知数据,把表格数据填写完整;
(II)利用(1)完成的表格数据回答下列问题:
(ⅰ)能否在犯错误的概率不超过0.001的前提下认为性别与支持申办足球世界杯有关;
(ⅱ)已知在被调查的支持申办足球世界杯的男性市民中有5位退休老人,其中2位是教师,现从这5位退休老人中随机抽取3人,求至多有1位老师的概率。
附:![]() ,其中
,其中![]()
| 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣ ![]() ,g(x)=ax+b.
,g(x)=ax+b.
(1)若函数h(x)=f(x)﹣g(x)在(0,+∞)上单调递增,求实数a的取值范围;
(2)若直线g(x)=ax+b是函数f(x)=lnx﹣ ![]() 图象的切线,求a+b的最小值;
图象的切线,求a+b的最小值;
(3)当b=0时,若f(x)与g(x)的图象有两个交点A(x1 , y1),B(x2 , y2),求证:x1x2>2e2 . (取e为2.8,取ln2为0.7,取 ![]() 为1.4)
为1.4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=x3+ax2+bx+1的导数![]() 满足
满足![]() ,
,![]() ,其中常数a,b∈R.
,其中常数a,b∈R.
(1)求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)设![]() ,求函数g(x)的极值.
,求函数g(x)的极值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个函数f(x),如果对任意一个三角形,只要它的三边长a,b,c都在f(x)的定义域内,就有f(a),f(b),f(c)也是某个三角形的三边长,则称f(x)为“三角保型函数”,给出下列函数: ①f(x)= ![]() ;②f(x)=x2;③f(x)=2x;④f(x)=lgx,
;②f(x)=x2;③f(x)=2x;④f(x)=lgx,
其中是“三角保型函数”的是( )
A.①②
B.①③
C.②③④
D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)的定义域为R,它的导函数y=f′(x)的部分图象如图所示,则下面结论正确的是( ) 
A.在(1,2)上函数f(x)为增函数
B.在(3,4)上函数f(x)为减函数
C.在(1,3)上函数f(x)有极大值
D.x=3是函数f(x)在区间[1,5]上的极小值点
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com