
| 5 |
| 3 |
| 2 |
| 3 |


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源: 题型:
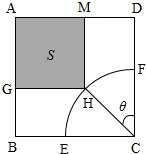 如图,体育馆计划用运动场的边角地建造一个矩形健身室,四边形ABCD是一块正方形地皮,边长为a(a>40m),扇形CEF是运动场的一部分,半径为40m,矩形AGHM就是计划的健身室,其中G、M分别在AB、AD上,H在
如图,体育馆计划用运动场的边角地建造一个矩形健身室,四边形ABCD是一块正方形地皮,边长为a(a>40m),扇形CEF是运动场的一部分,半径为40m,矩形AGHM就是计划的健身室,其中G、M分别在AB、AD上,H在 |
| EF |
 |
| EF |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 9 |
| 4 |
| AB |
| a |
| 2 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com