
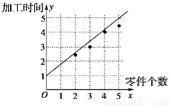
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
零件的个数 | 2 | 3 | 4 | 5 |
加工的时间 | 2.5 | 3 | 4 | 4.5 |
(1)在给定的坐标系中画出表中数据的散点图;
(2)求出 关于
关于 的线性回归方程
的线性回归方程 ,并在坐标系中画出回归直线;
,并在坐标系中画出回归直线;
(3)试预测加工 个零件需要多少时间?
个零件需要多少时间?
参考公式:回归直线 ,其中
,其中 .
.

(1)见图;(2)线性回归方程为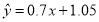 ,回归直线见图;(3)预测加工
,回归直线见图;(3)预测加工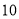 个零件需要
个零件需要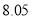 小时.
小时.
【解析】
试题分析:(1)画散点图,即根据提供的数对,找出对应的点即可,这一点不难;(2)首先要了解提供的计算公式中每个部分的含义,然后分步计算,这样做的好处在于出错时便于检查是哪步出错了,也能分步得分;(3)若了解回归方程的意义和作用,此问也不难,这一题对回归分析这部分内容考查的比较全面,其实关键还是落实在知识的理解和计算能力上.
试题解析:(1)散点图如下图.
 3分
3分
(2)由表中数据得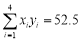 ,
,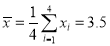 ,
,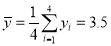 ,
,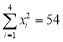
所以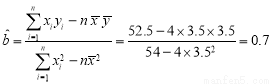 ,
,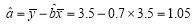 9分
9分
因此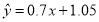 回归直线如图中所示. 10分
回归直线如图中所示. 10分
(3)将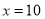 代入回归直线方程,得
代入回归直线方程,得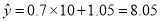 (小时),
(小时),
∴预测加工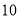 个零件需要
个零件需要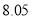 小时. 12分
小时. 12分
考点:线性回归方程及其应用.


科目:高中数学 来源:2015届广东省高二下学期中段考理科数学试卷(解析版) 题型:选择题
由数字0,1,2,3,4可组成无重复数字的两位数的个数是( )
A.25 B.20 C.16 D.12
查看答案和解析>>
科目:高中数学 来源:2015届广东省高二下学期中段考文科数学试卷(解析版) 题型:选择题
记I为虚数集,设 ,
, ,
, 。则下列类比所得的结论正确的是( )
。则下列类比所得的结论正确的是( )
A.由 ,类比得
,类比得
B.由 ,类比得
,类比得
C.由 ,类比得
,类比得
D.由 ,类比得
,类比得
查看答案和解析>>
科目:高中数学 来源:2015届广东省高二下学期期末考试理科数学试卷(解析版) 题型:选择题
一个袋中装有大小相同的5个白球和3个红球,现在不放回的取2次球,每次取出一个球,记“第1次拿出的是白球”为事件 ,“第2次拿出的是白球”为事件
,“第2次拿出的是白球”为事件 ,则事件
,则事件 与
与 同时发生的概率是( )
同时发生的概率是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com