
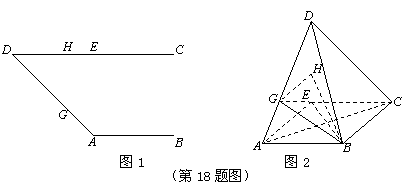
如图1,直角梯形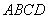 中,
中,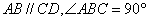 ,
,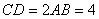 ,
, .
.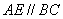 交
交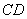 于点
于点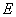 ,点
,点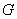 ,
,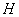 分别在线段
分别在线段 ,
, 上,且
上,且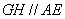 . 将图1中的
. 将图1中的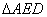 沿
沿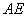 翻折,使平面
翻折,使平面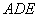 ⊥平面
⊥平面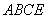 (如图2所示),连结
(如图2所示),连结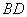 、
、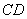 ,
,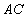 、
、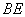 .
.
(Ⅰ)求证:平面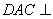 平面
平面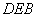 ;
;
 (Ⅱ)当三棱锥
(Ⅱ)当三棱锥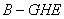 的体积最大时,求直线
的体积最大时,求直线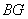 与平面
与平面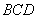 所成角的正弦值.
所成角的正弦值.
解:(Ⅰ)∵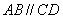 ,
,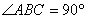 ,
,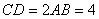
又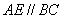 交
交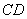 于点
于点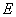 .
.
∴四边形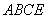 是边长为2的正方形 ………………………1分
是边长为2的正方形 ………………………1分
∴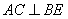 ,
, .
.
又∵平面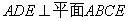
平面
∴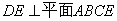 ………………………3分
………………………3分
∵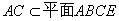 ,∴
,∴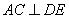 ……………………4分
……………………4分
又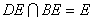
∴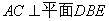 ………………………5分
………………………5分
∵
∴平面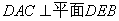 ………………………6分
………………………6分
(Ⅱ)由(Ⅰ)知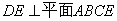 ,
,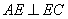
以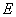 为原点,
为原点,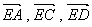 的方向为
的方向为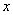 轴,
轴,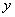 轴,
轴, 轴的正方向建立空间直角坐标系. ………………………7分
轴的正方向建立空间直角坐标系. ………………………7分
则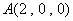 ,
,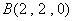 ,
,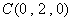 ,
,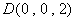
设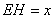 ,则
,则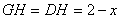 (
(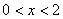 )
)
∵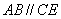 ,∴
,∴ …………………8分
…………………8分
∴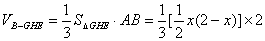
 ………………………9分
………………………9分
∵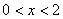 ,∴
,∴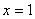 时,三棱锥
时,三棱锥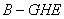 体积最大,此时,
体积最大,此时,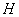 为
为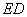 中点.
中点.
∵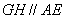 ,∴
,∴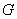 也是
也是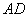 的中点,∴
的中点,∴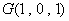 ,
,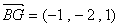 .…10分
.…10分
设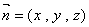 是面
是面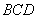 的法向量.
的法向量.
则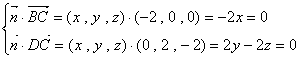
令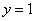 ,得
,得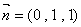 ………………………11分
………………………11分
设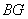 与面
与面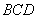 所成角为
所成角为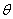
则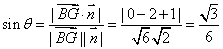
∴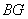 与平面
与平面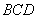 所成角的正弦值为
所成角的正弦值为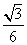 . ………………………13分
. ………………………13分


科目:高中数学 来源: 题型:
某班有34位同学,座位号记为01,02,…34,用下面的随机数表选取5组数作为参加青年志愿者活动的五位同学的座号.选取方法是从随机数表第一行的第6列和第7列数字开始,由左到右依次选取两个数字,则选出来的第4个志愿者的座号是

A.23 B.09 C.02 D.16
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)是在(0,+∞)上处处可导的函数,若xf ′(x)>f(x)在x>0上恒成立:
(1)判断函数g(x)=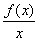 在(0,+∞)上的单调性;
在(0,+∞)上的单调性;
(2)当x1>0,x2>0时,证明f(x1)+f(x2)<f(x1+x2);
(3)求证: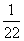 ln22+
ln22+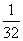 ln32+
ln32+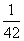 ln42+…
ln42+… 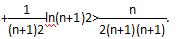
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com