
【题目】已知函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)若![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)答案见解析;(2) ![]() .
.
【解析】试题分析: ![]() 先求出导函数,结合定义域分类讨论
先求出导函数,结合定义域分类讨论![]() 、
、![]() 时的单调性(2)转化为最小值大于
时的单调性(2)转化为最小值大于![]() ,结合(1)中结果,分别求出最小值即可算出实数
,结合(1)中结果,分别求出最小值即可算出实数![]() 的取值范围
的取值范围
解析:(1)由题得, ![]() 的定义域为
的定义域为![]() ,
,
当![]() 时,
时, ![]() 恒成立,
恒成立,
故![]() 在区间
在区间![]() 上单调递减,无递增区间;
上单调递减,无递增区间;
当![]() ,由
,由![]() ,得
,得![]() ,
,
由![]() ,得
,得![]() .
.
所以![]() 的单调递减区间为
的单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]() .
.
(2)若![]() 恒成立,
恒成立,
即![]() 在区间
在区间![]() 上的最小值大于等于0,
上的最小值大于等于0,
由(1)可知,当![]() 时,
时, ![]() 恒成立,
恒成立,
即![]() 在区间
在区间![]() 上单调递减,
上单调递减,
故![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() ,
,
由![]() ,得
,得![]() ,故
,故![]() ,
,
当![]() 时,
时,
若![]() ,即
,即![]() 时,
时, ![]() 对
对![]() 恒成立,
恒成立,
所以![]() 在区间
在区间![]() 上单调递减,
上单调递减,
则![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() ,
,
显然![]() 的区间
的区间![]() 上的最小值大于等于0成立.
上的最小值大于等于0成立.
②若![]() ,即
,即![]() 时,则有
时,则有
|
|
|
|
| - | 0 | + |
|
| 极小值 |
|
所以![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() ,
,
由![]() ,得
,得![]() ,
,
解得![]() ,即
,即![]() .
.
综上所述,实数![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】已知f(x)=xln x,g(x)=x3+ax2-x+2.
(1)如果函数g(x)在区间![]() 上单调递减,求实数a的取值范围;
上单调递减,求实数a的取值范围;
(2)对任意x∈(0,+∞),2f(x)≤g′(x)+2恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a=(sinx,cosx),b=(sinx,sinx),f(x)=2a·b.
(1)求f(x)的最小正周期和最大值;
(2)若g(x)=f(x),x∈![]() ,画出函数y=g(x)的图象,讨论y=g(x)-m(m∈R)的零点个数.
,画出函数y=g(x)的图象,讨论y=g(x)-m(m∈R)的零点个数.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出以下四个说法:
①残差点分布的带状区域的宽度越窄相关指数越小
②在刻画回归模型的拟合效果时,相关指数![]() 的值越大,说明拟合的效果越好;
的值越大,说明拟合的效果越好;
③在回归直线方程![]() 中,当解释变量
中,当解释变量![]() 每增加一个单位时,预报变量
每增加一个单位时,预报变量![]() 平均增加
平均增加![]() 个单位;
个单位;
④对分类变量![]() 与
与![]() ,若它们的随机变量
,若它们的随机变量![]() 的观测值
的观测值![]() 越小,则判断“
越小,则判断“![]() 与
与![]() 有关系”的把握程度越大.
有关系”的把握程度越大.
其中正确的说法是![]()
A. ①④B. ②④C. ①③D. ②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《山东省高考改革试点方案》规定:从2017年秋季高中入学的新生开始,不分文理科;2020年开始,高考总成绩由语数外3门统考科目和物理、化学等六门选考科目构成.将每门选考科目的考生原始成绩从高到低划分为A、B+、B、C+、C、D+、D、E共8个等级.参照正态分布原则,确定各等级人数所占比例分别为3%、7%、16%、24%、24%、16%、7%、3%.选考科目成绩计入考生总成绩时,将A至E等级内的考生原始成绩,依照等比例转换法则,分别转换到[91,100]、[81,90]、[71,80]、[61,70]、[51,60]、[41,50]、[31,40]、[21,30]八个分数区间,得到考生的等级成绩.
某校高一年级共2000人,为给高一学生合理选科提供依据,对六个选考科目进行测试,其中物理考试原始成绩基本服从正态分布N(60,169).
(Ⅰ)求物理原始成绩在区间(47,86)的人数;
(Ⅱ)按高考改革方案,若从全省考生中随机抽取3人,记X表示这3人中等级成绩在区间[61,80]的人数,求X的分布列和数学期望.
(附:若随机变量![]() ,则
,则![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】CPI是居民消费价格指数(consumer price index)的简称.居民消费价格指数,是一个反映居民家庭一般所购买的消费品价格水平变动情况的宏观经济指标.右图是根据统计局发布的2018年1月—7月的CPI 同比增长与环比增长涨跌幅数据绘制的折线图.(注:2018 年2月与2017年2月相比较,叫同比;2018年2 月与2018年1月相比较,叫环比)根据该折线图,则下列结论错误的是( )
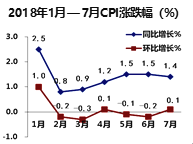
A. 2018年1月—7月CPI 有涨有跌
B. 2018年2月—7月CPI 涨跌波动不大,变化比较平稳
C. 2018年1月—7月分别与2017年1月一7月相比较,1月CPI 涨幅最大
D. 2018年1月—7月分别与2017年1月一7月相比较,CPI 有涨有跌
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() (a>b>0)的离心率
(a>b>0)的离心率![]() ,过点
,过点![]() 和
和![]() 的直线与原点的距离为
的直线与原点的距离为![]() .
.

(1)求椭圆的方程.
(2)已知定点![]() ,若直线
,若直线![]() 与椭圆交于C、D两点.问:是否存在k的值,使以CD为直径的圆过E点?请说明理由.
与椭圆交于C、D两点.问:是否存在k的值,使以CD为直径的圆过E点?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() :
:![]() ,点
,点![]() .
.
(1)求点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 的坐标;
的坐标;
(2)直线![]() 关于点
关于点![]() 对称的直线
对称的直线![]() 的方程;
的方程;
(3)以![]() 为圆心,3为半径长作圆,直线
为圆心,3为半径长作圆,直线![]() 过点
过点![]() ,且被圆
,且被圆![]() 截得的弦长为
截得的弦长为![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com