
【题目】如图,已知椭圆![]() (a>b>0)的离心率
(a>b>0)的离心率![]() ,过点
,过点![]() 和
和![]() 的直线与原点的距离为
的直线与原点的距离为![]() .
.

(1)求椭圆的方程.
(2)已知定点![]() ,若直线
,若直线![]() 与椭圆交于C、D两点.问:是否存在k的值,使以CD为直径的圆过E点?请说明理由.
与椭圆交于C、D两点.问:是否存在k的值,使以CD为直径的圆过E点?请说明理由.
【答案】(1)![]() ;(2)存在
;(2)存在![]() ,使得以
,使得以![]() 为直径的圆过点
为直径的圆过点![]() .
.
【解析】
试题分析:(1)由![]() 两点的坐标可得直线
两点的坐标可得直线![]() 方程,根据点到线的距离公式可得
方程,根据点到线的距离公式可得![]() 间的关系式,再结合离心率及
间的关系式,再结合离心率及![]() 可解得
可解得![]() 的值.(2)将直线方程与椭圆方程联立消去
的值.(2)将直线方程与椭圆方程联立消去![]() 整理为关于
整理为关于![]() 的一元二次方程.根据有2个交点可知其判别式大于0得
的一元二次方程.根据有2个交点可知其判别式大于0得![]() 的范围.由上式可得两根之和,两根之积.以
的范围.由上式可得两根之和,两根之积.以![]() 为直径的圆过点
为直径的圆过点![]() 时
时![]() ,根据直线垂直斜率相乘等于
,根据直线垂直斜率相乘等于![]() 可得
可得![]() 的值.若满足前边判别式大于0得的
的值.若满足前边判别式大于0得的![]() 的范围说明存在,否则说明不存在.
的范围说明存在,否则说明不存在.
试题解析:解:解析:(1)直线![]() 方程为:
方程为:![]() .
.
依题意 解得
解得 
∴ 椭圆方程为![]() .
.
(2)假若存在这样的![]() 值,由
值,由 得
得![]()
![]() .
.
∴ ![]() ①
①
设![]() ,
,![]() 、
、![]() ,
,![]() ,则
,则 ②
②
而![]() .
.
要使以![]() 为直径的圆过点
为直径的圆过点![]() ,当且仅当
,当且仅当![]() 时,则
时,则![]() ,即
,即![]()
∴![]() ③
③
将②式代入③整理解得![]() .经验证,
.经验证,![]() ,使①成立.
,使①成立.
综上可知,存在![]() ,使得以
,使得以![]() 为直径的圆过点
为直径的圆过点![]() .
.


科目:高中数学 来源: 题型:
【题目】某县城出租车的收费标准是:起步价是![]() 元(乘车不超过
元(乘车不超过![]() 千米);行驶
千米);行驶![]() 千米后,每千米车费1.2元;行驶
千米后,每千米车费1.2元;行驶![]() 千米后,每千米车费1.8元.
千米后,每千米车费1.8元.
(1)写出车费与路程的关系式;
(2)一顾客计划行程![]() 千米,为了省钱,他设计了三种乘车方案:
千米,为了省钱,他设计了三种乘车方案:
①不换车:乘一辆出租车行![]() 千米;
千米;
②分两段乘车:先乘一辆车行![]() 千米,换乘另一辆车再行
千米,换乘另一辆车再行![]() 千米;
千米;
③分三段乘车:每乘![]() 千米换一次车.
千米换一次车.
问哪一种方案最省钱.
查看答案和解析>>
科目:高中数学 来源: 题型:
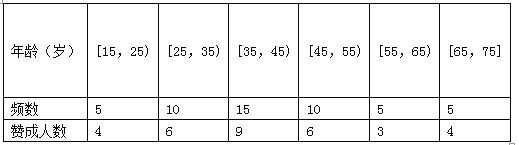
【题目】私家车的尾气排放是造成雾霾天气的重要因素之一,因此在生活中我们应该提倡低碳生活,少开私家车,尽量选择绿色出行方式,为预防雾霾出一份力.为此,很多城市实施了机动车车尾号限行,我市某报社为了解市区公众对“车辆限行”的态度,随机抽查了50人,将调查情况进行整理后制成下表:
(Ⅰ)完成被调查人员的频率分布直方图;
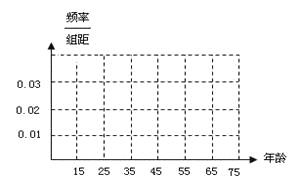
(Ⅱ)若从年龄在[15,25),[25,35)的被调查者中各随机选取2人进行追踪调查,求恰有2人不赞成的概率;
(Ⅲ)在(Ⅱ)的条件下,再记选中的4人中不赞成“车辆限行”的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】线段AB的两端在直二面角α-l-β的两个面内,并与这两个面都成30°角,则异面直线AB与l所成的角是( )
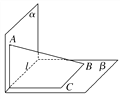
A. 30° B. 45°
C. 60° D. 75°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若在定义域内存在实数
,若在定义域内存在实数![]() ,满足
,满足![]() ,则称为“局部奇函数”
,则称为“局部奇函数”
(1)已知二次函数![]() (
(![]() 且
且![]() ),试判断
),试判断![]() 是否为“局部奇函数”,并说明理由;
是否为“局部奇函数”,并说明理由;
(2)若![]() 是定义在区间
是定义在区间![]() 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数![]() 的取值范围;
的取值范围;
(3)若![]() 为定义域为
为定义域为![]() 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数![]() 的取值范围;
的取值范围;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图![]() ,在直角梯形
,在直角梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,点
,点![]() 是
是![]() 边的中点,将
边的中点,将![]() 沿
沿![]() 折起,使平面
折起,使平面![]() 平面
平面![]() ,连接
,连接![]() ,
, ![]() ,
, ![]() ,得到如图
,得到如图![]() 所示的几何体.
所示的几何体.
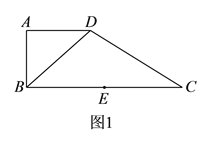
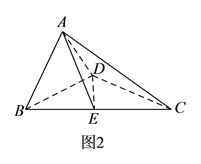
(Ⅰ)求证: ![]() 平面
平面![]() .
.
(Ⅱ)若![]() ,
, ![]() 与其在平面
与其在平面![]() 内的正投影所成角的正切值为
内的正投影所成角的正切值为![]() ,求点
,求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com