
【题目】在四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() 和
和![]() 都是边长为2的等边三角形,设
都是边长为2的等边三角形,设![]() 在底面
在底面![]() 的射影为
的射影为![]() .
.
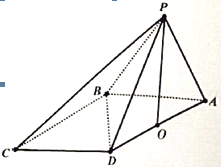
(1)求证:![]() 是
是![]() 中点;
中点;
(2)证明:![]() ;
;
(3)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)详见解析;(2)详见解析;(3)![]() .
.
【解析】试题分析:(1)根据等边三角形有![]() ,依题意有
,依题意有![]() 平面
平面![]() ,故
,故![]() ,由此可知
,由此可知![]() 为
为![]() 中点.(2)由
中点.(2)由![]() 平面
平面![]() 可得
可得![]() ,而
,而![]() ,即
,即![]() ,故
,故![]() 平面
平面![]() ,故
,故![]() .(3)以
.(3)以![]() 分别为
分别为![]() 轴建立空间直角坐标系,利用法向量计算二面角的余弦值.
轴建立空间直角坐标系,利用法向量计算二面角的余弦值.
试题解析:(1)证明:∵![]() 和
和![]() 都是等边三角形,
都是等边三角形,
∴![]() ,
,
又∵![]() 底面
底面![]() ,
,
∴![]() ,
,
则点![]() 为
为![]() 的外心,又因为
的外心,又因为![]() 是直角三角形,
是直角三角形,
∴点![]() 为
为![]() 中点.
中点.
(2)证明:由(1)知,点![]() 在底面的射影为点
在底面的射影为点![]() ,点
,点![]() 为
为![]() 中点,
中点,
于是![]() 面
面![]() ,
,
∴![]() ,
,
∵在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
又![]() ,∴
,∴![]() ,
,
从而![]() 即
即![]() ,
,
由![]() ,
,![]() 得
得![]() 面
面![]() ,
,
∴![]() .
.
(3)以点![]() 为原点,以
为原点,以![]() 所在射线为
所在射线为![]() 轴 ,
轴 ,![]() 轴,
轴,![]() 轴建系如图,
轴建系如图,
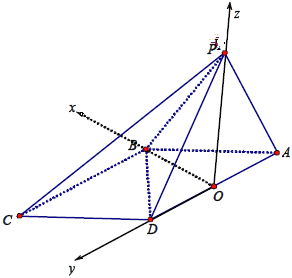
∵![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设面![]() 的法向量为
的法向量为![]() ,则
,则
![]() ,
,![]() ,得
,得![]() ,
,![]() ,
,
取![]() ,得
,得![]() ,
,![]() ,
,
故![]() .
.
设面![]() 的法向量为
的法向量为![]() ,则
,则
![]() ,
,![]() ,得
,得![]() ,
,![]() ,
,
取![]() ,则
,则![]() ,故
,故![]() ,
,
于是![]() ,
,
由图观察知![]() 为钝二面角,
为钝二面角,
所以该二面角的余弦值为![]() .
.


 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源: 题型:
【题目】社会公众人物的言行一定程度上影响着年轻人的人生观、价值观.某媒体机构为了解大学生对影视、歌星以及著名主持人方面的新闻(简称:“星闻”)的关注情况,随机调查了某大学的![]() 位大学生,得到信息如下表:
位大学生,得到信息如下表:
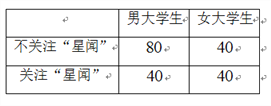
(Ⅰ)从所抽取的![]() 人内关注“星闻”的大学生中,再抽取三人做进一步调查,求这三人性别不全相同的概率;
人内关注“星闻”的大学生中,再抽取三人做进一步调查,求这三人性别不全相同的概率;
(Ⅱ)是否有![]() 以上的把握认为“关注‘星闻’与性别有关”,并说明理由;
以上的把握认为“关注‘星闻’与性别有关”,并说明理由;
(Ⅲ)把以上的频率视为概率,若从该大学随机抽取![]() 位男大学生,设这
位男大学生,设这![]() 人中关注“星闻”的人数为
人中关注“星闻”的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
附: 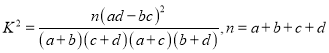 .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面给出四种说法:
①用相关指数R2来刻画回归效果,R2越小,说明模型的拟合效果越好;
②命题P:“x0∈R,x02﹣x0﹣1>0”的否定是¬P:“x∈R,x2﹣x﹣1≤0”;
③设随机变量X服从正态分布N(0,1),若P(x>1)=p则P(﹣1<X<0)=![]() ﹣p
﹣p
④回归直线一定过样本点的中心(![]() ).
).
其中正确的说法有( )
A. ①②③ B. ①②④ C. ②③④ D. ①②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修![]() :坐标系与参数方程
:坐标系与参数方程
已知曲线C的极坐标方程为ρ﹣4cosθ+3ρsin2θ=0,以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,直线l过点M(1,0),倾斜角为![]() .
.
(Ⅰ)求曲线C的直角坐标方程与直线l的参数方程;
(Ⅱ)若曲线C经过伸缩变换![]() 后得到曲线C′,且直线l与曲线C′交于A,B两点,求|MA|+|MB|.
后得到曲线C′,且直线l与曲线C′交于A,B两点,求|MA|+|MB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2015高考天津,文20】已知函数![]()
(I)求![]() 的单调区间;
的单调区间;
(II)设曲线![]() 与
与![]() 轴正半轴的交点为P,曲线在点P处的切线方程为
轴正半轴的交点为P,曲线在点P处的切线方程为![]() ,求证:对于任意的正实数
,求证:对于任意的正实数![]() ,都有
,都有![]() ;
;
(III)若方程![]() 有两个正实数根
有两个正实数根![]() 且
且![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某企业生产的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得如下频率分布直方图:
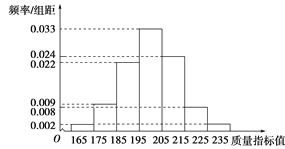
(1)求这500件产品质量指标值的样本平均数![]() 和样本方差s2(同一组中的数据用该组区间的中点值作代表);
和样本方差s2(同一组中的数据用该组区间的中点值作代表);
(2)由直方图可以认为,这种产品的质量指标值Z服从正态分布N(μ,σ2),其中μ近似为样本平均数![]() ,σ2近似为样本方差s2.
,σ2近似为样本方差s2.
(ⅰ)利用该正态分布,求P(187.8<Z<212.2);
(ⅱ)某用户从该企业购买了100件这种产品,记X表示这100件产品中质量指标值位于区间(187.8,212.2)的产品件数.利用(ⅰ)的结果,求E(X).
附: ![]() ≈12.2.若Z~N(μ,σ2),则P(μ-σ<Z<μ+σ)=0.682 6,P(μ-2σ<Z<μ+2σ)=0.954 4.
≈12.2.若Z~N(μ,σ2),则P(μ-σ<Z<μ+σ)=0.682 6,P(μ-2σ<Z<μ+2σ)=0.954 4.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() (a>b>0)的离心率
(a>b>0)的离心率![]() ,过点
,过点![]() 和
和![]() 的直线与原点的距离为
的直线与原点的距离为![]() .
.

(1)求椭圆的方程.
(2)已知定点![]() ,若直线
,若直线![]() 与椭圆交于C、D两点.问:是否存在k的值,使以CD为直径的圆过E点?请说明理由.
与椭圆交于C、D两点.问:是否存在k的值,使以CD为直径的圆过E点?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com